Description

Solves the eigenvalue problem with a direct method: first does LU factorization of Cq jacobians to find the null space, then solves the problem using the direct Eigen::EigenSolver.

Note: since intermediate dense matrices are built, the performance is acceptable only for small-sized problems. Note: since the method is direct, all eigenvalues are computed, regardless of n_modes, but only lower n_modes are returned.

#include <ChEigenvalueSolver.h>

Inheritance diagram for chrono::modal::ChQuadraticEigenvalueSolverNullspaceDirect:

[legend]

Collaboration diagram for chrono::modal::ChQuadraticEigenvalueSolverNullspaceDirect:

[legend]

Public Member Functions
virtual bool	Solve (const ChSparseMatrix &M, const ChSparseMatrix &R, const ChSparseMatrix &K, const ChSparseMatrix &Cq, ChMatrixDynamic< std::complex< double >> &eigvects, ChVectorDynamic< std::complex< double >> &eigvals, ChVectorDynamic< double > &freq, ChVectorDynamic< double > &damping_ratio, ChEigenvalueSolverSettings settings=0) const override
	Solve the quadratic eigenvalue problem (lambda^2M + lambdaR + K)*x = 0 s.t. More...

virtual bool	Solve (ChAssembly &assembly, ChMatrixDynamic< std::complex< double >> &eigvects, ChVectorDynamic< std::complex< double >> &eigvals, ChVectorDynamic< double > &freq, ChVectorDynamic< double > &damping_ratio, ChEigenvalueSolverSettings settings=0) const override
	Solve the quadratic eigenvalue problem (lambda^2M + lambdaR + K)*x = 0 s.t. More...

Public Member Functions inherited from chrono::modal::ChQuadraticEigenvalueSolver
double	GetTimeMatrixAssembly () const
	Get cumulative time for matrix assembly.

double	GetTimeEigenSetup () const
	Get cumulative time eigensolver setup.

double	GetTimeEigenSolver () const
	Get cumulative time eigensolver solution.

double	GetTimeSolutionPostProcessing () const
	Get cumulative time for post-solver solution postprocessing.

Additional Inherited Members
Protected Attributes inherited from chrono::modal::ChQuadraticEigenvalueSolver
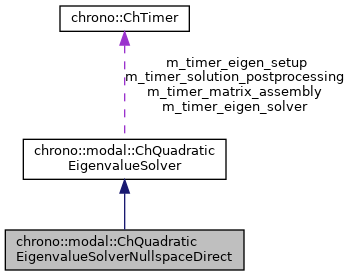
ChTimer	m_timer_matrix_assembly
	timer for matrix assembly

ChTimer	m_timer_eigen_setup
	timer for eigensolver setup

ChTimer	m_timer_eigen_solver
	timer for eigensolver solution

ChTimer	m_timer_solution_postprocessing
	timer for conversion of eigensolver solution

Member Function Documentation

◆ Solve() [1/2]

virtual bool chrono::modal::ChQuadraticEigenvalueSolverNullspaceDirect::Solve	(	ChAssembly &	assembly,
		ChMatrixDynamic< std::complex< double >> &	eigvects,
		ChVectorDynamic< std::complex< double >> &	eigvals,
		ChVectorDynamic< double > &	freq,
		ChVectorDynamic< double > &	damping_ratio,
		ChEigenvalueSolverSettings	settings = `0`
	)		const

inlineoverridevirtual

Solve the quadratic eigenvalue problem (lambda^2*M + lambda*R + K)*x = 0 s.t.

Cq*x = 0 If n_modes=0, return all eigenvalues, otherwise only the first lower n_modes.

Parameters

assembly	assembly on which to apply the eigen solver
eigvects	output matrix with eigenvectors as columns, will be resized
eigvals	output vector with eigenvalues (real part not zero if some damping), will be resized
freq	output vector with n undamped frequencies [Hz], as f=w/(2*PI), will be resized.
damping_ratio	output vector with n damping rations r=damping/critical_damping.
settings	optional: settings for the solver, or n. of desired lower eigenvalues. If =0, return all eigenvalues.

Implements chrono::modal::ChQuadraticEigenvalueSolver.

◆ Solve() [2/2]

bool chrono::modal::ChQuadraticEigenvalueSolverNullspaceDirect::Solve	(	const ChSparseMatrix &	M,
		const ChSparseMatrix &	R,
		const ChSparseMatrix &	K,
		const ChSparseMatrix &	Cq,
		ChMatrixDynamic< std::complex< double >> &	eigvects,
		ChVectorDynamic< std::complex< double >> &	eigvals,
		ChVectorDynamic< double > &	freq,
		ChVectorDynamic< double > &	damping_ratio,
		ChEigenvalueSolverSettings	settings = `0`
	)		const

overridevirtual