Description

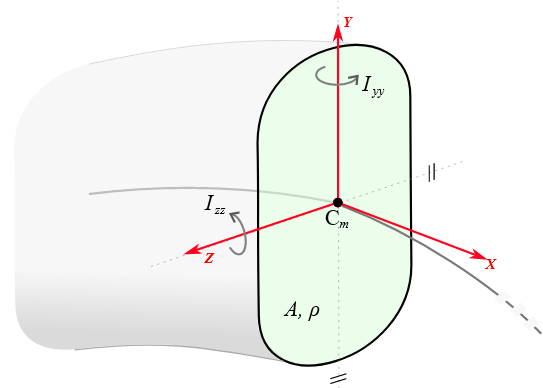
Inertia properties of a beam of Cosserat type, defined from an uniform density [kg/m^3], and the following geometric information:

a section area
Iyy Izz second moments of area The polar moment of area is automatically inferred via perpendicular axis theorem, Ip=Iyy+Izz. The section is assumed aligned to principal axis of the moment of area tensor, ie. Iyz=0, The section is assumed to be centered in the center of mass, The density is constant.

#include <ChBeamSectionCosserat.h>

Inheritance diagram for chrono::fea::ChInertiaCosseratSimple:

[legend]

Collaboration diagram for chrono::fea::ChInertiaCosseratSimple:

[legend]

Public Member Functions
	ChInertiaCosseratSimple (double density, double Area, double Iyy_area_moment, double Izz_area_moment)

virtual void	ComputeInertiaMatrix (ChMatrix66d &Mi) override
	Compute the 6x6 sectional inertia matrix, as in {x_momentum,w_momentum}=[Mi]{xvel,wvel} The matrix is computed in the material reference (i.e. More...

virtual void	ComputeInertiaDampingMatrix (ChMatrix66d &Ri, const ChVector3d &mW) override
	Compute the 6x6 sectional inertia damping matrix [Ri] (gyroscopic matrix damping), as in linearization dFi=[Mi]d{xacc,wacc}+[Ri]d{xvel,wvel}+[Ki]*d{pos,rot} The matrix is computed in the material reference, i.e. More...

virtual void	ComputeInertiaStiffnessMatrix (ChMatrix66d &Ki, const ChVector3d &mWvel, const ChVector3d &mWacc, const ChVector3d &mXacc) override
	Compute the 6x6 sectional inertia stiffness matrix [Ki^], as in linearization dFi=[Mi]d{xacc,wacc}+[Ri]d{xvel,wvel}+[Ki]*d{pos,rot} The matrix is computed in the material reference. More...

virtual void	ComputeQuadraticTerms (ChVector3d &mF, ChVector3d &mT, const ChVector3d &mW) override
	Compute the values of inertial torque depending on quadratic velocity terms, per unit length, that is the gyroscopic torque w x [J]w . More...

virtual double	GetMassPerUnitLength () override
	Compute mass per unit length, ex.SI units [kg/m] In this case is simply \( \mu = \rho A \), given area in [m^2] and with \( \rho \) density in [kg/m^3].

virtual double	GetInertiaJxxPerUnitLength ()
	Compute the Jxx component of the inertia tensor per unit length, i.e. More...

virtual double	GetInertiaJyyPerUnitLength ()
	Compute the Jyy component of the inertia tensor per unit length, i.e. More...

virtual double	GetInertiaJzzPerUnitLength ()
	Compute the Jzz component of the inertia tensor per unit length, i.e. More...

void	SetDensity (const double md)
	Set the volumetric density, assumed constant in the section. Ex. SI units: [kg/m^3].

double	GetDensity () const

void	SetArea (const double ma)
	Set the area of section for computing mass properties. Ex. SI units: [m^2].

double	GetArea () const

void	SetIyy (double mi)
	Set the Iyy second moment of area of the beam (for bending about y in xz plane), defined as \( I_{yy} = \int_\Omega z^2 d\Omega \). More...

double	GetIyy () const

void	SetIzz (double mi)
	Set the Izz second moment of area of the beam (for bending about z in xy plane), defined as \( I_{zz} = \int_\Omega y^2 d\Omega \). More...

double	GetIzz () const

virtual void	SetAsRectangularSection (double width_y, double width_z, double density)
	Shortcut: set Izz, Iyy, Area and density at once, given the y and z widths of the beam assumed with rectangular shape, and volumetric density. More...

virtual void	SetAsCircularSection (double diameter, double density)
	Shortcut: set Izz, Iyy, Area and density at once, given the diameter the beam assumed with circular shape, and volumetric density. More...

Public Member Functions inherited from chrono::fea::ChInertiaCosserat
virtual void	ComputeInertialForce (ChVector3d &mFi, ChVector3d &mTi, const ChVector3d &mWvel, const ChVector3d &mWacc, const ChVector3d &mXacc)
	Compute the total inertial wrench, ie forces and torques (per unit length). More...

Additional Inherited Members
Public Attributes inherited from chrono::fea::ChInertiaCosserat
ChBeamSectionCosserat *	section

bool	compute_inertia_damping_matrix = true
	Flag that turns on/off the computation of the [Ri] 'gyroscopic' inertial damping matrix. More...

bool	compute_inertia_stiffness_matrix = true
	Flag that turns on/off the computation of the [Ki] inertial stiffness matrix. More...

bool	compute_Ri_Ki_by_num_diff = false
	Flag for computing the Ri and Ki matrices via numerical differentiation even if an analytical expression is provided. More...

Constructor & Destructor Documentation

◆ ChInertiaCosseratSimple()

chrono::fea::ChInertiaCosseratSimple::ChInertiaCosseratSimple	(	double	density,
		double	Area,
		double	Iyy_area_moment,
		double	Izz_area_moment
	)

inline

Parameters

density	the density fo the material [kg/m^3], assumed constant
Area	area of the section, [m^2]
Iyy_area_moment	second moment of area [m^4] about Y
Izz_area_moment	second moment of area [m^4] about Z

Member Function Documentation

◆ ComputeInertiaDampingMatrix()

void chrono::fea::ChInertiaCosseratSimple::ComputeInertiaDampingMatrix	(	ChMatrix66d &	Ri,
		const ChVector3d &	mW
	)

overridevirtual

Compute the 6x6 sectional inertia damping matrix [Ri] (gyroscopic matrix damping), as in linearization dFi=[Mi]*d{xacc,wacc}+[Ri]*d{xvel,wvel}+[Ki]*d{pos,rot} The matrix is computed in the material reference, i.e.

both linear and rotational coords assumed in the basis of the centerline reference.

Parameters

Ri	6x6 sectional inertial-damping (gyroscopic damping) matrix values here
mW	current angular velocity of section, in material frame

Reimplemented from chrono::fea::ChInertiaCosserat.

◆ ComputeInertiaMatrix()

void chrono::fea::ChInertiaCosseratSimple::ComputeInertiaMatrix ( ChMatrix66d & Mi )

overridevirtual

Compute the 6x6 sectional inertia matrix, as in {x_momentum,w_momentum}=[Mi]{xvel,wvel} The matrix is computed in the material reference (i.e.

it is the sectional mass matrix). In this case it is simply a constant diagonal mass matrix with diagonal {rho*A,rho*A,rho*A, rho*Iyy+Izz, rho*Iyy, rho*Izz}

Parameters

Mi	6x6 sectional mass matrix values here

Implements chrono::fea::ChInertiaCosserat.

◆ ComputeInertiaStiffnessMatrix()

void chrono::fea::ChInertiaCosseratSimple::ComputeInertiaStiffnessMatrix	(	ChMatrix66d &	Ki,
		const ChVector3d &	mWvel,
		const ChVector3d &	mWacc,
		const ChVector3d &	mXacc
	)

overridevirtual

Compute the 6x6 sectional inertia stiffness matrix [Ki^], as in linearization dFi=[Mi]*d{xacc,wacc}+[Ri]*d{xvel,wvel}+[Ki]*d{pos,rot} The matrix is computed in the material reference.

NOTE the matrix already contains the 'geometric' stiffness, so it transforms to absolute transl/local rot just like [Mi] and [Ri]: [Ki]_al =[R,0;0,I]*[Ki^]*[R',0;0,I'] , with [Ki^]=([Ki]+[0,f~';0,0]) for f=current force part of inertial forces.

Parameters

Ki	6x6 sectional inertial-stiffness matrix [Ki^] values here
mWvel	current angular velocity of section, in material frame
mWacc	current angular acceleration of section, in material frame
mXacc	current acceleration of section, in material frame (not absolute!)

Reimplemented from chrono::fea::ChInertiaCosserat.

◆ ComputeQuadraticTerms()

void chrono::fea::ChInertiaCosseratSimple::ComputeQuadraticTerms	(	ChVector3d &	mF,
		ChVector3d &	mT,
		const ChVector3d &	mW
	)

overridevirtual

Compute the values of inertial torque depending on quadratic velocity terms, per unit length, that is the gyroscopic torque w x [J]w .

Quadratic force is null as mass is centered. All terms expressed in the material reference, ie. the reference in the centerline of the section.

Parameters

mF	centrifugal term (if any) returned here
mT	gyroscopic term returned here
mW	current angular velocity of section, in material frame

Implements chrono::fea::ChInertiaCosserat.

◆ GetInertiaJxxPerUnitLength()

virtual double chrono::fea::ChInertiaCosseratSimple::GetInertiaJxxPerUnitLength ( )

inlinevirtual

Compute the Jxx component of the inertia tensor per unit length, i.e.

the part associated with rotation about the beam direction. In this case it is \( J_{xx} = \rho I_p \), where \( I_p = I_{zz} + I_{yy} \) is the polar moment of area.

◆ GetInertiaJyyPerUnitLength()

virtual double chrono::fea::ChInertiaCosseratSimple::GetInertiaJyyPerUnitLength ( )

inlinevirtual

Compute the Jyy component of the inertia tensor per unit length, i.e.

the part associated with rotation of the section on its Y axis. Defined as: \( J_{yy} = \int_\Omega \rho z^2 d\Omega \), with \( \rho \) density in [kg/m^3]. For uniform density it is \( J_{yy} = \rho I_{yy} \), where \( I_{yy} = \int_\Omega z^2 d\Omega \) is the second moment of area.

◆ GetInertiaJzzPerUnitLength()

virtual double chrono::fea::ChInertiaCosseratSimple::GetInertiaJzzPerUnitLength ( )

inlinevirtual

Compute the Jzz component of the inertia tensor per unit length, i.e.

the part associated with rotation of the section on its Z axis. Defined as: \( J_{zz} = \int_\Omega \rho y^2 d\Omega \), with \( \rho \) density in [kg/m^3]. For uniform density it is \( J_{zz} = \rho I_{zz} \), where \( I_{zz} = \int_\Omega y^2 d\Omega \) is the second moment of area.

◆ SetAsCircularSection()

void chrono::fea::ChInertiaCosseratSimple::SetAsCircularSection	(	double	diameter,
		double	density
	)

virtual

Shortcut: set Izz, Iyy, Area and density at once, given the diameter the beam assumed with circular shape, and volumetric density.

Assuming centered section.

◆ SetAsRectangularSection()

void chrono::fea::ChInertiaCosseratSimple::SetAsRectangularSection	(	double	width_y,
		double	width_z,
		double	density
	)

virtual

Shortcut: set Izz, Iyy, Area and density at once, given the y and z widths of the beam assumed with rectangular shape, and volumetric density.

Assuming centered section.

◆ SetIyy()

void chrono::fea::ChInertiaCosseratSimple::SetIyy ( double mi )

inline

Set the Iyy second moment of area of the beam (for bending about y in xz plane), defined as \( I_{yy} = \int_\Omega z^2 d\Omega \).

Note: some textbook calls this Iyy as Iy. Note: it can correspond to the same Iyy that you used for the elasticity, ex. in ChElasticityCosseratSimple. Ex. SI units: [m^4]

◆ SetIzz()

void chrono::fea::ChInertiaCosseratSimple::SetIzz ( double mi )

inline

Set the Izz second moment of area of the beam (for bending about z in xy plane), defined as \( I_{zz} = \int_\Omega y^2 d\Omega \).

Note: some textbook calls this Izz as Iz. Note: it can correspond to the same Izz that you used for the elasticity, ex. in ChElasticityCosseratSimple. Ex. SI units: [m^4]

The documentation for this class was generated from the following files:

/builds/uwsbel/chrono/src/chrono/fea/ChBeamSectionCosserat.h
/builds/uwsbel/chrono/src/chrono/fea/ChBeamSectionCosserat.cpp

Description

Public Member Functions

Additional Inherited Members

Constructor & Destructor Documentation

◆ ChInertiaCosseratSimple()

Member Function Documentation

◆ ComputeInertiaDampingMatrix()

◆ ComputeInertiaMatrix()

◆ ComputeInertiaStiffnessMatrix()

◆ ComputeQuadraticTerms()

◆ GetInertiaJxxPerUnitLength()

◆ GetInertiaJyyPerUnitLength()

◆ GetInertiaJzzPerUnitLength()

◆ SetAsCircularSection()

◆ SetAsRectangularSection()

◆ SetIyy()

◆ SetIzz()