Description
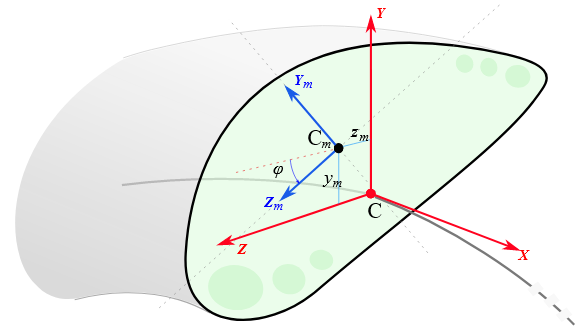
Inertia properties of a beam of Cosserat type, not necessarily of uniform density, from the following information that allows the center of mass to be offset respect to the beam centerline:
- a mass per unit length
- offset of the center of mass Cm along Y Z section axes,
- rotation of axes Y_m Z_m (used for computed Jzz_m Jyy_m) respect to Y Z section axes.
- Jyy_m Jzz_m principal moments of inertia computed in reference Y_m Z_m, rotated and with origin in center of mass Cm The polar moment of area is automatically inferred via perpendicular axis theorem.
#include <ChBeamSectionCosserat.h>
Public Member Functions | |
| ChInertiaCosseratMassref (double mu_density, double c_y, double c_z, double phi_massref, double Jyy_massref, double Jzz_massref) | |
| virtual void | SetInertiasPerUnitLength (double Jyy_moment, double Jzz_moment, double Jyz_moment) override |
| Set inertia moments, assumed computed in the Y Z unrotated reference frame of the section at centerline, and defined as: \( J_{yy} = \int_\Omega \rho z^2 d\Omega \), also Jyy = Mm(4,4) \( J_{zz} = \int_\Omega \rho y^2 d\Omega \), also Jzz = Mm(5,5) \( J_{yz} = \int_\Omega \rho y z d\Omega \), also Jyz = -Mm(4,5) = -Mm(5,4) Note that for an uniform density, these are also related to second moments of area as \( J_{yy} = \rho I_{yy} \), \( J_{zz} = \rho I_{zz} \). More... | |
| virtual void | SetMainInertiasInMassReference (double Jyy_massref, double Jzz_massref, double phi_massref) override |
| Set inertia moments as assumed computed in the Ym Zm "mass reference" frame, ie. More... | |
| virtual void | GetMainInertiasInMassReference (double &Jyy_massref, double &Jzz_massref, double &phi_massref) override |
| Get inertia moments as assumed computed in the Ym Zm "mass reference" frame, and the rotation phi of that frame, ie. More... | |
 Public Member Functions inherited from chrono::fea::ChInertiaCosseratAdvanced Public Member Functions inherited from chrono::fea::ChInertiaCosseratAdvanced | |
| ChInertiaCosseratAdvanced (double mu_density, double c_y, double c_z, double Jyy_moment, double Jzz_moment, double Jyz_moment) | |
| virtual void | ComputeInertiaMatrix (ChMatrixNM< double, 6, 6 > &M) override |
| Compute the 6x6 sectional inertia matrix, as in {x_momentum,w_momentum}=[Mm]{xvel,wvel} The matrix is computed in the material reference (i.e. More... | |
| virtual void | ComputeQuadraticTerms (ChVector<> &mF, ChVector<> &mT, const ChVector<> &mW) override |
| Compute the values of inertial force & torque depending on quadratic velocity terms, that is the gyroscopic torque w x [J]w and the centrifugal term (if center of mass is offset). More... | |
| virtual double | GetMassPerUnitLength () override |
| Get mass per unit length, ex.SI units [kg/m]. | |
| virtual void | SetMassPerUnitLength (double mmu) |
| Set mass c, ex.SI units [kg/m]. More... | |
| void | SetCenterOfMass (double my, double mz) |
| "mass reference": set the displacement of the center of mass respect to the section centerline reference. | |
| double | GetCenterOfMassY () |
| double | GetCenterOfMassZ () |
| virtual double | GetInertiaJxxPerUnitLength () |
| Get the Jxx component of the inertia per unit length (polar inertia), in the Y Z unrotated reference frame of the section at centerline. More... | |
| virtual double | GetInertiaJyyPerUnitLength () |
| Get the Jyy component of the inertia per unit length, in the Y Z unrotated reference frame of the section at centerline, also Jyy = Mm(4,4) | |
| virtual double | GetInertiaJzzPerUnitLength () |
| Get the Jzz component of the inertia per unit length, in the Y Z unrotated reference frame of the section at centerline, also Jzz = Mm(5,5) | |
| virtual double | GetInertiaJyzPerUnitLength () |
| Get the Jyz off-diagonal component of the inertia per unit length, in the Y Z unrotated reference frame of the section at centerline. More... | |
Additional Inherited Members | |
 Public Attributes inherited from chrono::fea::ChInertiaCosserat Public Attributes inherited from chrono::fea::ChInertiaCosserat | |
| ChBeamSectionCosserat * | section |
Constructor & Destructor Documentation
◆ ChInertiaCosseratMassref()
|
inline |
- Parameters
-
mu_density mass per unit length [kg/m] c_y displacement of center of mass Cm along Y c_z displacement of center of mass Cm along Z phi_massref rotation of auxiliary mass reference Ym Zm respect to Y Z reference Jyy_massref moment of inertia per unit length, about Ym, with origin in Cm Jzz_massref moment of inertia per unit length, about Zm, with origin in Cm
Member Function Documentation
◆ GetMainInertiasInMassReference()
|
inlineoverridevirtual |
Get inertia moments as assumed computed in the Ym Zm "mass reference" frame, and the rotation phi of that frame, ie.
inertias centered at the center of mass and rotated by phi angle to match the main axes of inertia: \( Jm_{yy} = \int_\Omega \rho z_{m}^2 d\Omega \), \( Jm_{zz} = \int_\Omega \rho y_{m}^2 d\Omega \). Assuming the center of mass is already set.
Reimplemented from chrono::fea::ChInertiaCosseratAdvanced.
◆ SetInertiasPerUnitLength()
|
inlineoverridevirtual |
Set inertia moments, assumed computed in the Y Z unrotated reference frame of the section at centerline, and defined as: \( J_{yy} = \int_\Omega \rho z^2 d\Omega \), also Jyy = Mm(4,4) \( J_{zz} = \int_\Omega \rho y^2 d\Omega \), also Jzz = Mm(5,5) \( J_{yz} = \int_\Omega \rho y z d\Omega \), also Jyz = -Mm(4,5) = -Mm(5,4) Note that for an uniform density, these are also related to second moments of area as \( J_{yy} = \rho I_{yy} \), \( J_{zz} = \rho I_{zz} \).
Note also that \( J_{xy} = J_{xz} = J_{yx} = J_{zx} = 0 \) anyway. Note also that \( J_{xy} \) does not need to be input, as automatically computed via \( J_{xx} = J_{yy} +J_{zz} \) for the polar theorem.
Reimplemented from chrono::fea::ChInertiaCosseratAdvanced.
◆ SetMainInertiasInMassReference()
|
inlineoverridevirtual |
Set inertia moments as assumed computed in the Ym Zm "mass reference" frame, ie.
centered at the center of mass and rotated by phi angle to match the main axes of inertia: \( Jm_{yy} = \int_\Omega \rho z_{m}^2 d\Omega \), \( Jm_{zz} = \int_\Omega \rho y_{m}^2 d\Omega \). Assuming the center of mass is already set.
Reimplemented from chrono::fea::ChInertiaCosseratAdvanced.
The documentation for this class was generated from the following file:
- /builds/uwsbel/chrono/src/chrono/fea/ChBeamSectionCosserat.h
