Description

Special subcase: II-order differential system.

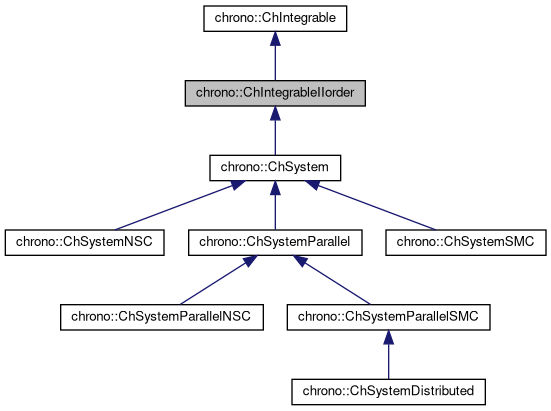
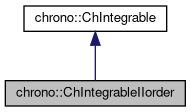
Interface class for all objects that support time integration with state y that is second order: y = {x, v} , dy/dt={v, a} with positions x, speeds v=dx/dt, and accelerations a=ddx/dtdt. Such systems permit the use of special integrators that can exploit the particular system structure.

#include <ChIntegrable.h>

Inheritance diagram for chrono::ChIntegrableIIorder:

[legend]

Collaboration diagram for chrono::ChIntegrableIIorder:

[legend]

Public Member Functions
virtual int	GetNcoords_x ()=0
	Return the number of position coordinates x in y = {x, v}.

virtual int	GetNcoords_v ()
	Return the number of speed coordinates of v in y = {x, v} and dy/dt={v, a} This is a base implementation that works in many cases where dim(v) = dim(x), but might be less ex. More...

virtual int	GetNcoords_a ()
	Return the number of acceleration coordinates of a in dy/dt={v, a} This is a default implementation that works in almost all cases, as dim(a) = dim(v),.

virtual void	StateSetup (ChState &x, ChStateDelta &v, ChStateDelta &a)
	Set up the system state with separate II order components x, v, a for y = {x, v} and dy/dt={v, a}.

virtual void	StateGather (ChState &x, ChStateDelta &v, double &T)
	From system to state y={x,v} Optionally, they will copy system private state, if any, to y={x,v}.

virtual void	StateScatter (const ChState &x, const ChStateDelta &v, const double T)
	Scatter the states from the provided arrays to the system. More...

virtual void	StateGatherAcceleration (ChStateDelta &a)
	Gather from the system the acceleration in specified array. More...

virtual void	StateScatterAcceleration (const ChStateDelta &a)
	Scatter the acceleration from the provided array to the system. More...

virtual bool	StateSolveA (ChStateDelta &Dvdt, ChVectorDynamic<> &L, const ChState &x, const ChStateDelta &v, const double T, const double dt, bool force_state_scatter=true)
	Solve for accelerations: a = f(x,v,t) Given current state y={x,v} , computes acceleration a in the state derivative dy/dt={v,a} and lagrangian multipliers L (if any). More...

virtual void	StateIncrementX (ChState &x_new, const ChState &x, const ChStateDelta &Dx)
	Increment state array: x_new = x + dx for x in Y = {x, dx/dt} This is a base implementation that works in many cases, but it can be overridden in the case that x contains quaternions for rotations NOTE: the system is not updated automatically after the state increment, so one might need to call StateScatter() if needed. More...

virtual bool	StateSolveCorrection (ChStateDelta &Dv, ChVectorDynamic<> &L, const ChVectorDynamic<> &R, const ChVectorDynamic<> &Qc, const double c_a, const double c_v, const double c_x, const ChState &x, const ChStateDelta &v, const double T, bool force_state_scatter=true, bool force_setup=true)
	Assuming an explicit ODE in the form Ma = F(x,v,t) Assuming an explicit DAE in the form Ma = F(x,v,t) + Cq'*L C(x,t) = 0 this must compute the solution of the change Du (in a or v or x) for a Newton iteration within an implicit integration scheme. More...

virtual void	LoadResidual_F (ChVectorDynamic<> &R, const double c) override
	Assuming Ma = F(x,v,t) + Cq'L C(x,t) = 0 increment a vector R (usually the residual in a Newton Raphson iteration for solving an implicit integration step) with the term cF: R += cF. More...

virtual void	LoadResidual_Mv (ChVectorDynamic<> &R, const ChVectorDynamic<> &w, const double c)
	Assuming Ma = F(x,v,t) + Cq'L C(x,t) = 0 increment a vector R (usually the residual in a Newton Raphson iteration for solving an implicit integration step) with a term that has M multiplied a given vector w: R += cMw. More...

virtual void	LoadResidual_CqL (ChVectorDynamic<> &R, const ChVectorDynamic<> &L, const double c) override
	Assuming Ma = F(x,v,t) + Cq'L C(x,t) = 0 increment a vectorR (usually the residual in a Newton Raphson iteration for solving an implicit integration step) with the term Cq'L: R += cCq'*L. More...

virtual void	LoadConstraint_C (ChVectorDynamic<> &Qc, const double c, const bool do_clamp=false, const double mclam=1e30) override
	Assuming Ma = F(x,v,t) + Cq'L C(x,t) = 0 Increment a vector Qc (usually the residual in a Newton Raphson iteration for solving an implicit integration step, constraint part) with the term C: Qc += c*C. More...

virtual void	LoadConstraint_Ct (ChVectorDynamic<> &Qc, const double c) override
	Assuming Ma = F(x,v,t) + Cq'L C(x,t) = 0 Increment a vector Qc (usually the residual in a Newton Raphson iteration for solving an implicit integration step, constraint part) with the term Ct = partial derivative dC/dt: Qc += c*Ct. More...

virtual int	GetNcoords_y () override
	Return the number of coordinates in the state Y. More...

virtual int	GetNcoords_dy () override
	Return the number of coordinates in the state increment. More...

virtual void	StateGather (ChState &y, double &T) override
	Gather system state in specified array. More...

virtual void	StateScatter (const ChState &y, const double T) override
	Scatter the states from the provided array to the system. More...

virtual void	StateGatherDerivative (ChStateDelta &Dydt) override
	Gather from the system the state derivatives in specified array. More...

virtual void	StateScatterDerivative (const ChStateDelta &Dydt) override
	Scatter the state derivatives from the provided array to the system. More...

virtual void	StateIncrement (ChState &y_new, const ChState &y, const ChStateDelta &Dy) override
	Increment state array: y_new = y + Dy. More...

virtual bool	StateSolve (ChStateDelta &dydt, ChVectorDynamic<> &L, const ChState &y, const double T, const double dt, bool force_state_scatter=true) override
	Solve for state derivatives: dy/dt = f(y,t). More...

virtual bool	StateSolveCorrection (ChStateDelta &Dy, ChVectorDynamic<> &L, const ChVectorDynamic<> &R, const ChVectorDynamic<> &Qc, const double a, const double b, const ChState &y, const double T, const double dt, bool force_state_scatter=true, bool force_setup=true) override
	This was for Ist order implicit integrators, but here we disable it.

Public Member Functions inherited from chrono::ChIntegrable
virtual int	GetNconstr ()
	Return the number of lagrangian multipliers (constraints). More...

virtual void	StateSetup (ChState &y, ChStateDelta &dy)
	Set up the system state.

virtual void	StateGatherReactions (ChVectorDynamic<> &L)
	Gather from the system the Lagrange multipliers in specified array. More...

virtual void	StateScatterReactions (const ChVectorDynamic<> &L)
	Scatter the Lagrange multipliers from the provided array to the system. More...

virtual void	LoadResidual_Hv (ChVectorDynamic<> &R, const ChVectorDynamic<> &v, const double c)
	Increment a vector R (usually the residual in a Newton Raphson iteration for solving an implicit integration step) with a term that has H multiplied a given vector w: R += cHw. More...

Member Function Documentation

◆ GetNcoords_dy()

virtual int chrono::ChIntegrableIIorder::GetNcoords_dy ( )

inlineoverridevirtual

Return the number of coordinates in the state increment.

(overrides base - just a fallback to enable using with plain 1st order timesteppers)

Reimplemented from chrono::ChIntegrable.

◆ GetNcoords_v()

virtual int chrono::ChIntegrableIIorder::GetNcoords_v ( )

inlinevirtual

Return the number of speed coordinates of v in y = {x, v} and dy/dt={v, a} This is a base implementation that works in many cases where dim(v) = dim(x), but might be less ex.

if x uses quaternions and v uses angular vel.

Reimplemented in chrono::ChSystem.

◆ GetNcoords_y()

virtual int chrono::ChIntegrableIIorder::GetNcoords_y ( )

inlineoverridevirtual

Return the number of coordinates in the state Y.

(overrides base - just a fallback to enable using with plain 1st order timesteppers)

Implements chrono::ChIntegrable.

◆ LoadConstraint_C()

virtual void chrono::ChIntegrableIIorder::LoadConstraint_C	(	ChVectorDynamic<> &	Qc,
		const double	c,
		const bool	do_clamp = `false`,
		const double	mclam = `1e30`
	)

inlineoverridevirtual

Assuming M*a = F(x,v,t) + Cq'*L C(x,t) = 0 Increment a vector Qc (usually the residual in a Newton Raphson iteration for solving an implicit integration step, constraint part) with the term C: Qc += c*C.

Parameters

Qc	result: the Qc residual, Qc += c*C
c	a scaling factor
do_clamp	enable optional clamping of Qc
mclam	clamping value

Reimplemented from chrono::ChIntegrable.

Reimplemented in chrono::ChSystem.

◆ LoadConstraint_Ct()

virtual void chrono::ChIntegrableIIorder::LoadConstraint_Ct	(	ChVectorDynamic<> &	Qc,
		const double	c
	)

inlineoverridevirtual

Assuming M*a = F(x,v,t) + Cq'*L C(x,t) = 0 Increment a vector Qc (usually the residual in a Newton Raphson iteration for solving an implicit integration step, constraint part) with the term Ct = partial derivative dC/dt: Qc += c*Ct.

Parameters

Qc	result: the Qc residual, Qc += c*Ct
c	a scaling factor

Reimplemented from chrono::ChIntegrable.

Reimplemented in chrono::ChSystem.

◆ LoadResidual_CqL()

virtual void chrono::ChIntegrableIIorder::LoadResidual_CqL	(	ChVectorDynamic<> &	R,
		const ChVectorDynamic<> &	L,
		const double	c
	)

inlineoverridevirtual

Assuming M*a = F(x,v,t) + Cq'*L C(x,t) = 0 increment a vectorR (usually the residual in a Newton Raphson iteration for solving an implicit integration step) with the term Cq'*L: R += c*Cq'*L.

Parameters

R	result: the R residual, R += cCq'L
L	the L vector
c	a scaling factor

Reimplemented from chrono::ChIntegrable.

Reimplemented in chrono::ChSystem.

◆ LoadResidual_F()

virtual void chrono::ChIntegrableIIorder::LoadResidual_F	(	ChVectorDynamic<> &	R,
		const double	c
	)

inlineoverridevirtual

Assuming M*a = F(x,v,t) + Cq'*L C(x,t) = 0 increment a vector R (usually the residual in a Newton Raphson iteration for solving an implicit integration step) with the term c*F: R += c*F.

Parameters

R	result: the R residual, R += c*F
c	a scaling factor

Reimplemented from chrono::ChIntegrable.

Reimplemented in chrono::ChSystem.

◆ LoadResidual_Mv()

virtual void chrono::ChIntegrableIIorder::LoadResidual_Mv	(	ChVectorDynamic<> &	R,
		const ChVectorDynamic<> &	w,
		const double	c
	)

inlinevirtual

Assuming M*a = F(x,v,t) + Cq'*L C(x,t) = 0 increment a vector R (usually the residual in a Newton Raphson iteration for solving an implicit integration step) with a term that has M multiplied a given vector w: R += c*M*w.

Parameters

R	result: the R residual, R += cMv
w	the w vector
c	a scaling factor

Reimplemented in chrono::ChSystem.

◆ StateGather()

void chrono::ChIntegrableIIorder::StateGather	(	ChState &	y,
		double &	T
	)

overridevirtual

Gather system state in specified array.

(overrides base - just a fallback to enable using with plain 1st order timesteppers) PERFORMANCE WARNING! temporary vectors allocated on heap. This is only to support compatibility with 1st order integrators.

Reimplemented from chrono::ChIntegrable.

◆ StateGatherAcceleration()

virtual void chrono::ChIntegrableIIorder::StateGatherAcceleration ( ChStateDelta & a )

inlinevirtual

Gather from the system the acceleration in specified array.

Optional: the integrable object might contain last computed state derivative, some integrators might use it.

Reimplemented in chrono::ChSystem.

◆ StateGatherDerivative()

void chrono::ChIntegrableIIorder::StateGatherDerivative ( ChStateDelta & Dydt )

overridevirtual

Gather from the system the state derivatives in specified array.

The integrable object might contain last computed state derivative, some integrators might reuse it. (overrides base - just a fallback to enable using with plain 1st order timesteppers) PERFORMANCE WARNING! temporary vectors allocated on heap. This is only to support compatibility with 1st order integrators.

Reimplemented from chrono::ChIntegrable.

◆ StateIncrement()

void chrono::ChIntegrableIIorder::StateIncrement	(	ChState &	y_new,
		const ChState &	y,
		const ChStateDelta &	Dy
	)

overridevirtual

Increment state array: y_new = y + Dy.

This is a base implementation that works in many cases. It calls StateIncrementX() if used on x in y={x, dx/dt}. It calls StateIncrementX() for x, and a normal sum for dx/dt if used on y in y={x, dx/dt}

Parameters

y_new	resulting y_new = y + Dy
y	initial state y
Dy	state increment Dy

Reimplemented from chrono::ChIntegrable.

◆ StateIncrementX()

void chrono::ChIntegrableIIorder::StateIncrementX	(	ChState &	x_new,
		const ChState &	x,
		const ChStateDelta &	Dx
	)

virtual

Increment state array: x_new = x + dx for x in Y = {x, dx/dt} This is a base implementation that works in many cases, but it can be overridden in the case that x contains quaternions for rotations NOTE: the system is not updated automatically after the state increment, so one might need to call StateScatter() if needed.

Parameters

x_new	resulting x_new = x + Dx
x	initial state x
Dx	state increment Dx

Reimplemented in chrono::ChSystem.

◆ StateScatter() [1/2]

virtual void chrono::ChIntegrableIIorder::StateScatter	(	const ChState &	x,
		const ChStateDelta &	v,
		const double	T
	)

inlinevirtual

Scatter the states from the provided arrays to the system.

This function is called by time integrators all times they modify the Y state. In some cases, the ChIntegrable object might contain dependent data structures that might need an update at each change of Y. If so, this function must be overridden.

Reimplemented in chrono::ChSystem.

◆ StateScatter() [2/2]

void chrono::ChIntegrableIIorder::StateScatter	(	const ChState &	y,
		const double	T
	)

overridevirtual

Scatter the states from the provided array to the system.

(overrides base - just a fallback to enable using with plain 1st order timesteppers) PERFORMANCE WARNING! temporary vectors allocated on heap. This is only to support compatibility with 1st order integrators.

Reimplemented from chrono::ChIntegrable.

◆ StateScatterAcceleration()

virtual void chrono::ChIntegrableIIorder::StateScatterAcceleration ( const ChStateDelta & a )

inlinevirtual

Scatter the acceleration from the provided array to the system.

Optional: the integrable object might contain last computed state derivative, some integrators might use it.

Reimplemented in chrono::ChSystem.

◆ StateScatterDerivative()

void chrono::ChIntegrableIIorder::StateScatterDerivative ( const ChStateDelta & Dydt )

overridevirtual

Scatter the state derivatives from the provided array to the system.

The integrable object might need to store last computed state derivative, ex. for plotting etc. NOTE! the velocity in dsdt={v,a} is not scattered to the II order integrable, only acceleration is scattered! (overrides base - just a fallback to enable using with plain 1st order timesteppers) PERFORMANCE WARNING! temporary vectors allocated on heap. This is only to support compatibility with 1st order integrators.

Reimplemented from chrono::ChIntegrable.

◆ StateSolve()

bool chrono::ChIntegrableIIorder::StateSolve	(	ChStateDelta &	dydt,
		ChVectorDynamic<> &	L,
		const ChState &	y,
		const double	T,
		const double	dt,
		bool	force_state_scatter = `true`
	)

overridevirtual

Solve for state derivatives: dy/dt = f(y,t).

(overrides base - just a fallback to enable using with plain 1st order timesteppers) PERFORMANCE WARNING! temporary vectors allocated on heap. This is only to support compatibility with 1st order integrators.

Parameters

dydt	result: computed dydt
L	result: computed lagrangian multipliers, if any
y	current state y
T	current time T
dt	timestep (if needed, ex. in DVI)
force_state_scatter	if false, y and T are not scattered to the system

Implements chrono::ChIntegrable.

◆ StateSolveA()

bool chrono::ChIntegrableIIorder::StateSolveA	(	ChStateDelta &	Dvdt,
		ChVectorDynamic<> &	L,
		const ChState &	x,
		const ChStateDelta &	v,
		const double	T,
		const double	dt,
		bool	force_state_scatter = `true`
	)

virtual

Solve for accelerations: a = f(x,v,t) Given current state y={x,v} , computes acceleration a in the state derivative dy/dt={v,a} and lagrangian multipliers L (if any).

NOTES

some solvers (ex in DVI) cannot compute a classical derivative dy/dt when v is a function of bounded variation, and f or L are distributions (e.g., when there are impulses and discontinuities), so they compute a finite Dv through a finite dt. This is the reason why this function has an optional parameter dt. In a DVI setting, one computes Dv, and returns Dv*(1/dt) here in Dvdt parameter; if the original Dv has to be known, just multiply Dvdt*dt later. The same for impulses: a DVI would compute impulses I, and return L=I*(1/dt).
derived classes must take care of calling StateScatter(y,T) before computing Dy, only if force_state_scatter = true (otherwise it is assumed state is already in sync)
derived classes must take care of resizing Dv if needed.

This function must return true if successful and false otherwise.

This default implementation uses the same functions already used for implicit integration. WARNING: this implementation avoids the computation of the analytical expression for Qc, but at the cost of three StateScatter updates.

Parameters

Dvdt	result: computed a for a=dv/dt
L	result: computed lagrangian multipliers, if any
x	current state, x
v	current state, v
T	current time T
dt	timestep (if needed)
force_state_scatter	if false, x,v and T are not scattered to the system

◆ StateSolveCorrection()

virtual bool chrono::ChIntegrableIIorder::StateSolveCorrection	(	ChStateDelta &	Dv,
		ChVectorDynamic<> &	L,
		const ChVectorDynamic<> &	R,
		const ChVectorDynamic<> &	Qc,
		const double	c_a,
		const double	c_v,
		const double	c_x,
		const ChState &	x,
		const ChStateDelta &	v,
		const double	T,
		bool	force_state_scatter = `true`,
		bool	force_setup = `true`
	)

inlinevirtual

Assuming an explicit ODE in the form M*a = F(x,v,t) Assuming an explicit DAE in the form M*a = F(x,v,t) + Cq'*L C(x,t) = 0 this must compute the solution of the change Du (in a or v or x) for a Newton iteration within an implicit integration scheme.

If in ODE case: Du = [ c_a*M + c_v*dF/dv + c_x*dF/dx ]^-1 * R Du = [ G ]^-1 * R If with DAE constraints: |Du| = [ G Cq' ]^-1 * | R | |DL| [ Cq 0 ] | Qc| where R is a given residual, dF/dv and dF/dx, dF/dv are jacobians (that are also -R and -K, damping and stiffness (tangent) matrices in many mechanical problems, note the minus sign!). It is up to the derived class how to solve such linear system.

This function must return true if successful and false otherwise.

Parameters

Dv	result: computed Dv
L	result: computed lagrangian multipliers, if any
R	the R residual
Qc	the Qc residual
c_a	the factor in c_a*M
c_v	the factor in c_v*dF/dv
c_x	the factor in c_x*dF/dv
x	current state, x part
v	current state, v part
T	current time T
force_state_scatter	if false, x,v and T are not scattered to the system
force_setup	if true, call the solver's Setup() function

Reimplemented in chrono::ChSystem.

The documentation for this class was generated from the following files:

/builds/uwsbel/chrono/src/chrono/timestepper/ChIntegrable.h
/builds/uwsbel/chrono/src/chrono/timestepper/ChIntegrable.cpp

Description

Public Member Functions

Member Function Documentation

◆ GetNcoords_dy()

◆ GetNcoords_v()

◆ GetNcoords_y()

◆ LoadConstraint_C()

◆ LoadConstraint_Ct()

◆ LoadResidual_CqL()

◆ LoadResidual_F()

◆ LoadResidual_Mv()

◆ StateGather()

◆ StateGatherAcceleration()

◆ StateGatherDerivative()

◆ StateIncrement()

◆ StateIncrementX()

◆ StateScatter() [1/2]

◆ StateScatter() [2/2]

◆ StateScatterAcceleration()

◆ StateScatterDerivative()

◆ StateSolve()

◆ StateSolveA()

◆ StateSolveCorrection()