Description

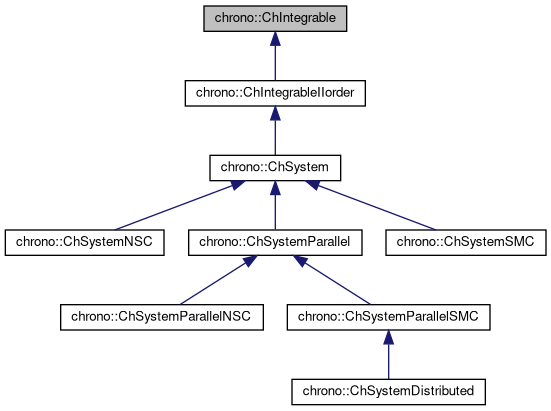
Interface class for all objects that support time integration.

Derived concrete classes can use time integrators for the ChTimestepper hierarchy.

#include <ChIntegrable.h>

Inheritance diagram for chrono::ChIntegrable:

[legend]

Public Member Functions
virtual int	GetNcoords_y ()=0
	Return the number of coordinates in the state Y.

virtual int	GetNcoords_dy ()
	Return the number of coordinates in the state increment. More...

virtual int	GetNconstr ()
	Return the number of lagrangian multipliers (constraints). More...

virtual void	StateSetup (ChState &y, ChStateDelta &dy)
	Set up the system state.

virtual void	StateGather (ChState &y, double &T)
	Gather system state in specified array. More...

virtual void	StateScatter (const ChState &y, const double T)
	Scatter the states from the provided array to the system. More...

virtual void	StateGatherDerivative (ChStateDelta &Dydt)
	Gather from the system the state derivatives in specified array. More...

virtual void	StateScatterDerivative (const ChStateDelta &Dydt)
	Scatter the state derivatives from the provided array to the system. More...

virtual void	StateGatherReactions (ChVectorDynamic<> &L)
	Gather from the system the Lagrange multipliers in specified array. More...

virtual void	StateScatterReactions (const ChVectorDynamic<> &L)
	Scatter the Lagrange multipliers from the provided array to the system. More...

virtual bool	StateSolve (ChStateDelta &Dydt, ChVectorDynamic<> &L, const ChState &y, const double T, const double dt, bool force_state_scatter=true)=0
	Solve for state derivatives: dy/dt = f(y,t). More...

virtual void	StateIncrement (ChState &y_new, const ChState &y, const ChStateDelta &Dy)
	Increment state array: y_new = y + Dy. More...

virtual bool	StateSolveCorrection (ChStateDelta &Dy, ChVectorDynamic<> &L, const ChVectorDynamic<> &R, const ChVectorDynamic<> &Qc, const double a, const double b, const ChState &y, const double T, const double dt, bool force_state_scatter=true, bool force_setup=true)
	Assuming an explicit ODE Hdy/dt = F(y,t) or an explicit DAE Hdy/dt = F(y,t) + Cq*L C(y,t) = 0 this function must compute the state increment as required for a Newton iteration within an implicit integration scheme. More...

virtual void	LoadResidual_Hv (ChVectorDynamic<> &R, const ChVectorDynamic<> &v, const double c)
	Increment a vector R (usually the residual in a Newton Raphson iteration for solving an implicit integration step) with a term that has H multiplied a given vector w: R += cHw. More...

virtual void	LoadResidual_F (ChVectorDynamic<> &R, const double c)
	Increment a vector R (usually the residual in a Newton Raphson iteration for solving an implicit integration step) with the term cF: R += cF. More...

virtual void	LoadResidual_CqL (ChVectorDynamic<> &R, const ChVectorDynamic<> &L, const double c)
	Increment a vector R (usually the residual in a Newton Raphson iteration for solving an implicit integration step) with the term Cq'L: R += cCq'*L. More...

virtual void	LoadConstraint_C (ChVectorDynamic<> &Qc, const double c, const bool do_clamp=false, const double mclam=1e30)
	Increment a vector Qc (usually the residual in a Newton Raphson iteration for solving an implicit integration step, constraint part) with the term C: Qc += c*C. More...

virtual void	LoadConstraint_Ct (ChVectorDynamic<> &Qc, const double c)
	Increment a vector Qc (usually the residual in a Newton Raphson iteration for solving an implicit integration step, constraint part) with the term Ct = partial derivative dC/dt: Qc += c*Ct. More...

Member Function Documentation

◆ GetNconstr()

virtual int chrono::ChIntegrable::GetNconstr ( )

inlinevirtual

Return the number of lagrangian multipliers (constraints).

By default returns 0.

Reimplemented in chrono::ChSystem.

◆ GetNcoords_dy()

virtual int chrono::ChIntegrable::GetNcoords_dy ( )

inlinevirtual

Return the number of coordinates in the state increment.

This is a base implementation that works in many cases where dim(Y) = dim(dy), but it can be overridden in the case that y contains quaternions for rotations rather than simple y+dy

Reimplemented in chrono::ChIntegrableIIorder.

◆ LoadConstraint_C()

virtual void chrono::ChIntegrable::LoadConstraint_C	(	ChVectorDynamic<> &	Qc,
		const double	c,
		const bool	do_clamp = `false`,
		const double	mclam = `1e30`
	)

inlinevirtual

Increment a vector Qc (usually the residual in a Newton Raphson iteration for solving an implicit integration step, constraint part) with the term C: Qc += c*C.

Parameters

Qc	result: the Qc residual, Qc += c*C
c	a scaling factor
do_clamp	enable optional clamping of Qc
mclam	clamping value

Reimplemented in chrono::ChSystem, and chrono::ChIntegrableIIorder.

◆ LoadConstraint_Ct()

virtual void chrono::ChIntegrable::LoadConstraint_Ct	(	ChVectorDynamic<> &	Qc,
		const double	c
	)

inlinevirtual

Increment a vector Qc (usually the residual in a Newton Raphson iteration for solving an implicit integration step, constraint part) with the term Ct = partial derivative dC/dt: Qc += c*Ct.

Parameters

Qc	result: the Qc residual, Qc += c*Ct
c	a scaling factor

Reimplemented in chrono::ChSystem, and chrono::ChIntegrableIIorder.

◆ LoadResidual_CqL()

virtual void chrono::ChIntegrable::LoadResidual_CqL	(	ChVectorDynamic<> &	R,
		const ChVectorDynamic<> &	L,
		const double	c
	)

inlinevirtual

Increment a vector R (usually the residual in a Newton Raphson iteration for solving an implicit integration step) with the term Cq'*L: R += c*Cq'*L.

Parameters

R	result: the R residual, R += cCq'L
L	the L vector
c	a scaling factor

Reimplemented in chrono::ChSystem, and chrono::ChIntegrableIIorder.

◆ LoadResidual_F()

virtual void chrono::ChIntegrable::LoadResidual_F	(	ChVectorDynamic<> &	R,
		const double	c
	)

inlinevirtual

Increment a vector R (usually the residual in a Newton Raphson iteration for solving an implicit integration step) with the term c*F: R += c*F.

Parameters

R	result: the R residual, R += c*F
c	a scaling factor

Reimplemented in chrono::ChSystem, and chrono::ChIntegrableIIorder.

◆ LoadResidual_Hv()

virtual void chrono::ChIntegrable::LoadResidual_Hv	(	ChVectorDynamic<> &	R,
		const ChVectorDynamic<> &	v,
		const double	c
	)

inlinevirtual

Increment a vector R (usually the residual in a Newton Raphson iteration for solving an implicit integration step) with a term that has H multiplied a given vector w: R += c*H*w.

Parameters

R	result: the R residual, R += cMv
v	the v vector
c	a scaling factor

◆ StateGather()

virtual void chrono::ChIntegrable::StateGather	(	ChState &	y,
		double &	T
	)

inlinevirtual

Gather system state in specified array.

Optionally, they will copy system private state, if any, to Y.

Reimplemented in chrono::ChIntegrableIIorder.

◆ StateGatherDerivative()

virtual void chrono::ChIntegrable::StateGatherDerivative ( ChStateDelta & Dydt )

inlinevirtual

Gather from the system the state derivatives in specified array.

Optional: the integrable object might contain last computed state derivative, some integrators might reuse it.

Reimplemented in chrono::ChIntegrableIIorder.

◆ StateGatherReactions()

virtual void chrono::ChIntegrable::StateGatherReactions ( ChVectorDynamic<> & L )

inlinevirtual

Gather from the system the Lagrange multipliers in specified array.

Optional: the integrable object might contain Lagrange multipliers (reaction in constraints)

Reimplemented in chrono::ChSystem.

◆ StateIncrement()

void chrono::ChIntegrable::StateIncrement	(	ChState &	y_new,
		const ChState &	y,
		const ChStateDelta &	Dy
	)

virtual

Increment state array: y_new = y + Dy.

This is a base implementation that works in many cases, but it can be overridden in the case that y contains quaternions for rotations, in which case rot. exponential is needed instead of simply doing y+Dy. NOTE: the system is not updated automatically after the state increment, so one might need to call StateScatter().

Parameters

y_new	resulting y_new = y + Dy
y	initial state y
Dy	state increment Dy

Reimplemented in chrono::ChIntegrableIIorder.

◆ StateScatter()

virtual void chrono::ChIntegrable::StateScatter	(	const ChState &	y,
		const double	T
	)

inlinevirtual

Scatter the states from the provided array to the system.

This function is called by time integrators every time they modify the Y state. In some cases, the ChIntegrable object might contain dependent data structures that might need an update at each change of Y. If so, this function must be overridden.

Reimplemented in chrono::ChIntegrableIIorder.

◆ StateScatterDerivative()

virtual void chrono::ChIntegrable::StateScatterDerivative ( const ChStateDelta & Dydt )

inlinevirtual

Scatter the state derivatives from the provided array to the system.

Optional: the integrable object might need to store last computed state derivative, ex. for plotting etc.

Reimplemented in chrono::ChIntegrableIIorder.

◆ StateScatterReactions()

virtual void chrono::ChIntegrable::StateScatterReactions ( const ChVectorDynamic<> & L )

inlinevirtual

Scatter the Lagrange multipliers from the provided array to the system.

Optional: the integrable object might contain Lagrange multipliers (reaction in constraints)

Reimplemented in chrono::ChSystem.

◆ StateSolve()

virtual bool chrono::ChIntegrable::StateSolve	(	ChStateDelta &	Dydt,
		ChVectorDynamic<> &	L,
		const ChState &	y,
		const double	T,
		const double	dt,
		bool	force_state_scatter = `true`
	)

pure virtual

Solve for state derivatives: dy/dt = f(y,t).

Given current state y , computes the state derivative dy/dt and Lagrange multipliers L (if any). NOTE: some solvers (ex in DVI) cannot compute a classical derivative dy/dt when v is a function of bounded variation, and f or L are distributions (e.g., when there are impulses and discontinuities), so they compute a finite Dy through a finite dt. This is the reason why this function has an optional parameter dt. In a DVI setting, one computes Dy, and returns Dy*(1/dt) here in Dydt parameter; if the original Dy has to be known, just multiply Dydt*dt. The same for impulses: a DVI would compute impulses I, and return L=I*(1/dt). NOTES:

derived classes must take care of calling StateScatter(y,T) before computing Dy, only if force_state_scatter = true (otherwise it is assumed state is already in sync)
derived classes must take care of resizing Dy and L if needed.

This function must return true if successful and false otherwise.

Parameters

Dydt	result: computed Dydt
L	result: computed lagrangian multipliers, if any
y	current state y
T	current time T
dt	timestep (if needed, ex. in DVI)
force_state_scatter	if false, y and T are not scattered to the system

Implemented in chrono::ChIntegrableIIorder.

◆ StateSolveCorrection()

virtual bool chrono::ChIntegrable::StateSolveCorrection	(	ChStateDelta &	Dy,
		ChVectorDynamic<> &	L,
		const ChVectorDynamic<> &	R,
		const ChVectorDynamic<> &	Qc,
		const double	a,
		const double	b,
		const ChState &	y,
		const double	T,
		const double	dt,
		bool	force_state_scatter = `true`,
		bool	force_setup = `true`
	)

inlinevirtual

Assuming an explicit ODE H*dy/dt = F(y,t) or an explicit DAE H*dy/dt = F(y,t) + Cq*L C(y,t) = 0 this function must compute the state increment as required for a Newton iteration within an implicit integration scheme.

For an ODE: Dy = [ c_a*H + c_b*dF/dy ]^-1 * R Dy = [ G ]^-1 * R For a DAE with constraints: |Dy| = [ G Cq' ]^-1 * | R | |DL| [ Cq 0 ] | Qc| where R is a given residual and dF/dy is the Jacobian of F.

This function must return true if successful and false otherwise.

Parameters

Dy	result: computed Dy
L	result: computed lagrangian multipliers, if any
R	the R residual
Qc	the Qc residual
a	the factor in c_a*H
b	the factor in c_b*dF/dy
y	current state y
T	current time T
dt	timestep (if needed)
force_state_scatter	if false, y and T are not scattered to the system
force_setup	if true, call the solver's Setup() function

Reimplemented in chrono::ChIntegrableIIorder.

The documentation for this class was generated from the following files:

/builds/uwsbel/chrono/src/chrono/timestepper/ChIntegrable.h
/builds/uwsbel/chrono/src/chrono/timestepper/ChIntegrable.cpp

Description

Public Member Functions

Member Function Documentation

◆ GetNconstr()

◆ GetNcoords_dy()

◆ LoadConstraint_C()

◆ LoadConstraint_Ct()

◆ LoadResidual_CqL()

◆ LoadResidual_F()

◆ LoadResidual_Hv()

◆ StateGather()

◆ StateGatherDerivative()

◆ StateGatherReactions()

◆ StateIncrement()

◆ StateScatter()

◆ StateScatterDerivative()

◆ StateScatterReactions()

◆ StateSolve()

◆ StateSolveCorrection()