Table of Contents
Chrono::Vehicle currently supports three different classes of tire models: rigid, handling, and finite element.
Rigid tire model
The rigid tires are the simplest of the three tire classes offered. The assumption for these models is that the tire is completely rigid and it interacts with the ground and any other rigid objects through the same underlying friction and contact algorithms as the other rigid bodies in Chrono. The contact geometry for these tires can be as simple as a cylinder or as complex as a 3D triangular mesh. These models are not only useful for debugging the overall vehicle model, but they can also be used in cases where runtime is important, the terrain is much softer than the tire, and a highly detailed model of the tire is unnecessary. In fact, the semi-empirical tire models are not suitable for off-road vehicle simulation, i.e. when using a deformable terrain (SCM, granular, or FEA-based; see the description of available terrain models). For such scenarios, rigid or FEA-based tire models are the only two available options currently implemented in Chrono::Vehicle.
See ChRigidTire and RigidTire.
The following is an example of a rigid tire with mesh geometry provided through a Wavefront OBJ file:
Handling (semi-empirical) tire models
The second class of tires models offered are the semi-empirical ones commonly used for vehicle handling. Chrono::Vehicle currently has implementations for Pacejka (89 and 2002), TMeasy, and Fiala tire models. Handling tire models are designed for flat road surfaces and they normally use single point contact or four point contact (TMeasy). For ride tests on ondulated roads or for obstacle crossing a special contact algorithm called "envelope" has been implemented. It is based on a paper of Sui & Hershey and can be used with all handling tire models that are included in Chrono. Validation tests with a technology demonstrator show good results compared to measured real vehicle test data with low numerical effort. If an even better accuracy is needed the user should think about considering FEA based tire models for non-handling tests.
Some users may want to build their own handling tire parameter sets from tire test data. Be sure to get familiar with the different slip definitions and the different coordinate systems in each tire model!
Pacejka 89 (Pac89) tire model
See ChPac89Tire and Pac89Tire.
Pacejka 2002 (Pac02) tire model
This model is an extension of Pacejka's earlier Magic Formula tire model with additional equations and coefficients. Since a large number of vehicle dynamics maneuvers do not occur under steady-state slip conditions, the contact patch slip state equations are included to provide more accurate results under transient conditions. Due to the lack of reference data sets the inflation pressure dependence terms and the large camber terms are actually not implemented.
This Chrono tire model can also be specified using Adams/Car-compatible TIR files.
See ChPac02Tire and Pac02Tire.
TMeasy tire model (basic version)
TMeasy (Tire Model Made Easy) has been developed by Prof. Dr. Georg Rill and is available as a commercial code (see http://www.tmeasy.de/ for more information). The aim of this model is to allow easy parametration. Its complexity is roughly comparable to the Magic Formula based models. Furthermore, based on known parameter sets for trucks and passenger cars it is possible to estimate a complete parameter set from few input data. TMeasy considers nonlinear effects and includes contact patch slip state equations. The implementation used in Chrono lacks some functionality compared to the latest commercial TMeasy versions. For example, there is no belt dynamics and no dynamic parking torque calculation possible. The Chrono TMeasy tire implementation contains algorithms that have been published in the book Road Vehicle Dynamics - Fundamentals and Modeling with MATLAB, Georg Rill and Abel Arrieta Castro, CRC Press, 2020.
See ChTMeasyTire and TMeasyTire.
A sample JSON file with a TMeasy tire specification is provided below:
Fiala tire model
The Fiala tire model implemented in Chrono::Vehicle is largely based on the transient Fiala tire model presented in the MSC ADAMS/tire help documentation, which uses tire slip state equations to improve the model's behavior at slow to zero forward velocities. The Fiala tire model is based on a brush model assumption and only requires a small number of coefficients. This tire model assumes that the tire is at zero camber with respect to the road and does not have any provisions for generating overturning moments. It does however couple the lateral and longitudinal slip states of the tire in its force and moment calculations, providing a more realistic description of combined slip. The Fiala tire model should not be used for serious vehicle handling simulations since it does not consider important effects that influence the results.
See ChFialaTire and FialaTire.
A sample JSON file with a TMeasy tire specification is provided below:
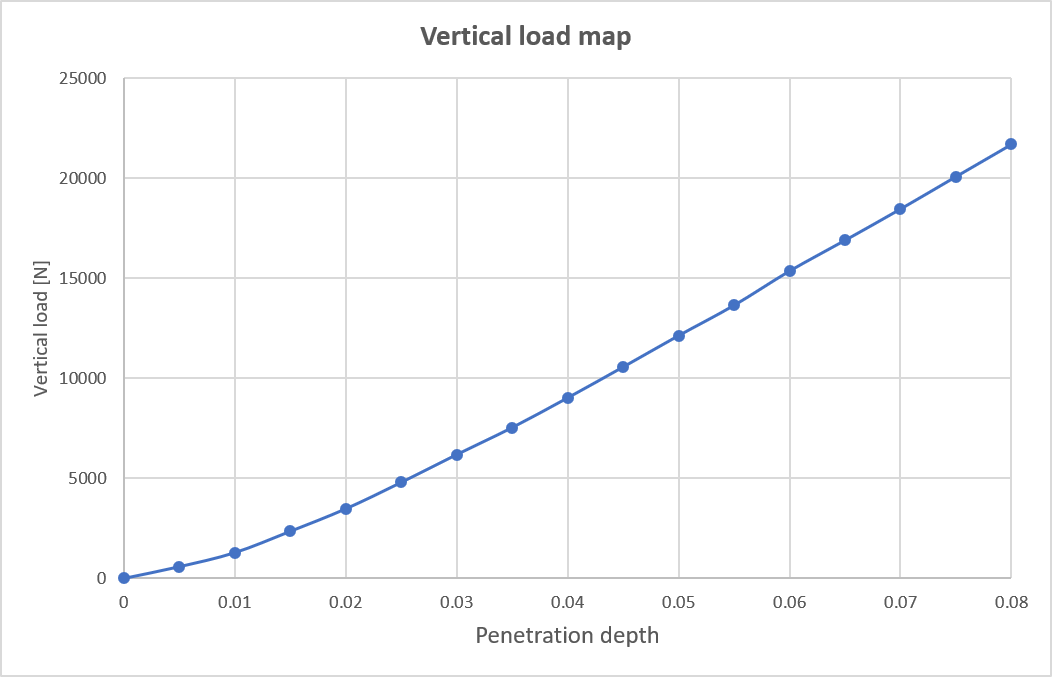
The vertical load curve embedded in the above JSON file is show below:
Validation of handling tire models
We show below a validation study for 3 of the Chrono::Vehicle handling tire models done against experimental data provided for the FED-alpha vehicle by the Keweenah Research Center (KRC) in Michigan.
In this test, called Steady State Cornering (SSC), the vehicle drives along a circle beginning with the so-called "Ackermann-Speed". This value is around 3 m/s, and as such the slip values are pretty small and the vehicle follows the circle kinematically. The real test continues by increasing the vehicle speed in steps and holding it constant. These successive speed increase steps are repeated until the maximal possible lateral acceleration is reached, or the engine power is exhausted. The KRC test was conducted in left turn and right turns, to highlight any asymmetry of the vehicle (if present).
The goal of the SSC test is to infer if a vehicle is safe for an average driver. The vehicle should understeer, meaning the driver must provide more and more turning angle of the steering wheel with increasing lateral acceleration to keep the vehicle on the circle and maintain vehicle stability. Vehicles which are "oversteering" tend to turn toward the circle origin and become unstable, because there is not enough lateral slip reserve at the rear wheels. This oversteering behavior should be avoided for standard vehicles used in public traffic by normal drivers, although professional rally drivers prefer the oversteerers.
For the FED-alpha, the SSC test has been defined as a quasi-steady-state run, where the speed changes continuously but very slowly, so that there are no noticeable dynamics effects. The simulation results are therefore shown as continuous lines. The signs of the data are chosen in a way that shows the right turn on the right side and the left turn on the left side. Experimental KRC data is represented with dots. The plots below show SSC simulation results for the Chrono Pac02, TMsimple, and TMeasy tire models superimposed over the KRC experimental data.
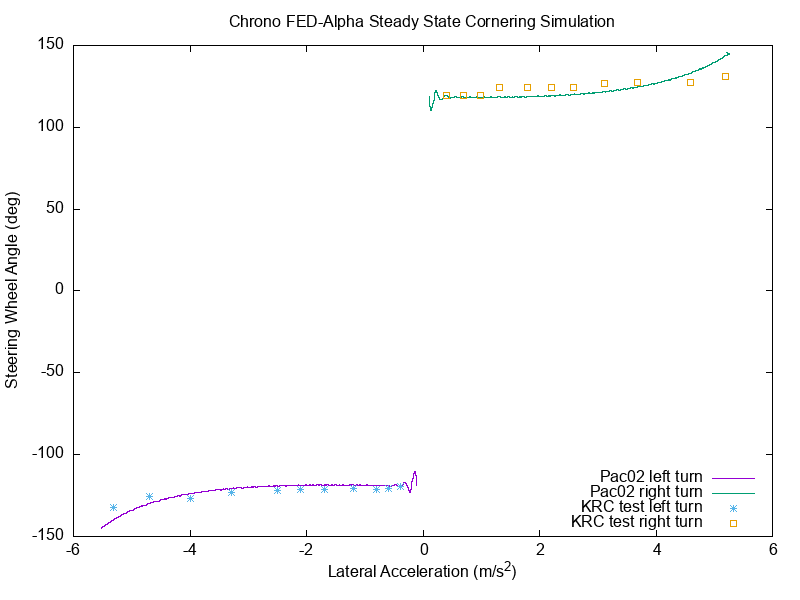
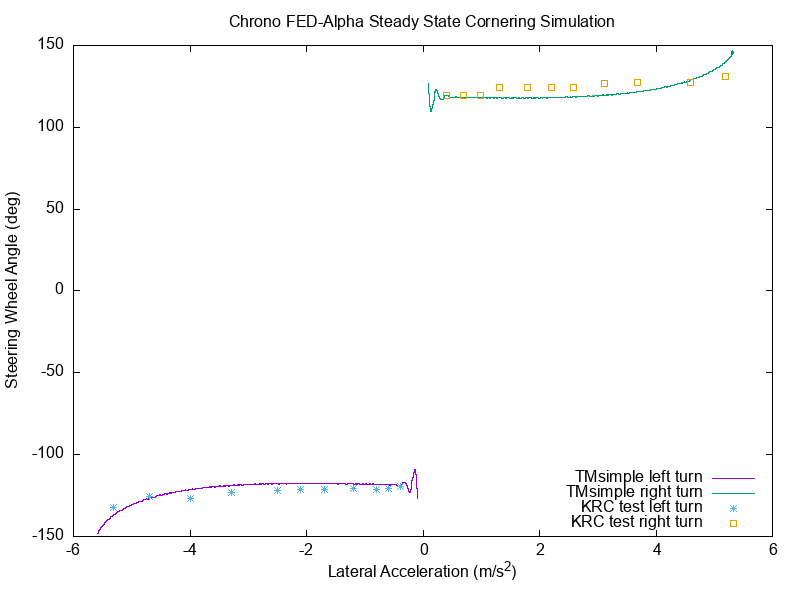
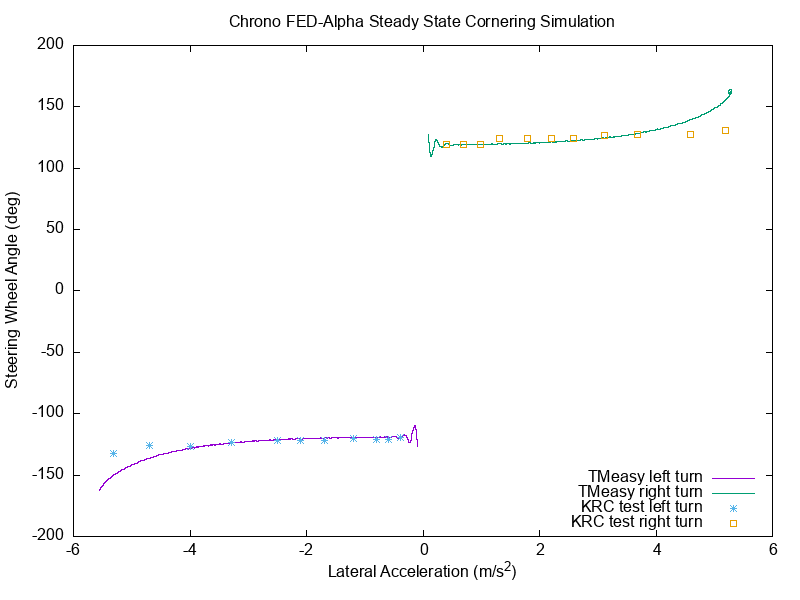
FEA-based tire models
Finally, the third class of tire models offered are full finite element representations of the tire. While these models have the potential to be the most accurate due to their detailed physical model of the tire, they are also the most computationally expensive of the tire model currently available in Chrono::Vehicle. Unlike the rigid or semi-empirical tire models, the finite element based tire models are able to account for the flexibility in both the tire and in the ground at the same time, which is an important characteristic for many types of off-road mobility and vehicle dynamics studies. These finite element tire models leverage the nonlinear finite element capabilities in Chrono.
ANCF shell deformable tire
See ChANCFTire and ANCFTire.
The following JSON file contains the specification of an ANCFTire:
Reissner shell deformable tire
See ChReissnerTire and ReissnerTire.
