ChSystem

A Chrono simulation system is an object of class ChSystem. See chrono::ChSystem for API details.

Note that ChSystem is an abstract class: you must instantiate one of its specializations. In detail you can use of these sublclasses:

A chrono::ChSystemNSC , for Non Smooth Contacts (NSC); in case of contacts a complementarity solver will take care of them using non smooth dynamics; this is very efficient even with large time steps.
A chrono::ChSystemSMC , for SMooth Contacts (SMC); with this system contacts are handled using penalty methods, i.e. contacts are deformable;

If there are no contacts or collisions in your system, it is indifferent to use ChSystemNSC or ChSystemSMC.

Example: The following picture shows how mechanisms turn into a database of bodies and links in a ChSystem:

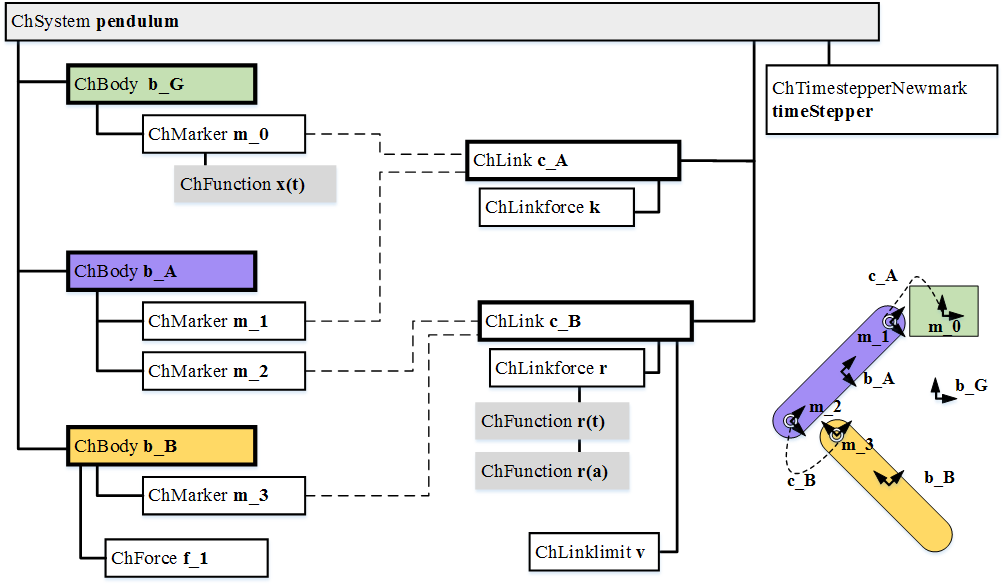
A chrono::ChSystem contains all items that participate in a simulation: bodies, constraints, numerical integrator type, integration tolerances, etc.
Use the Add(), Remove() functions to add elements to a system object

Recommended way of dealing with system objects:

Create a chrono::ChSystemNSC or a chrono::ChSystemSMC
Add body objects into it, see chrono::ChBody
Add link objects into it, see chrono::ChLink
Adjust parameters for the time integration
Run a dynamics simulation of a certain length

Example: a slider-crank mechanism

// 1- Create a Chrono physical system: all bodies and constraints
//    will belong to and be handled by this ChSystemNSC object.
ChSystemNSC my_system;
 
 
// 2- Create the rigid bodies of the slider-crank 
//   (a crank, a rod, a truss), possibly setting their position/mass/inertias attributes
    
// ..the truss
auto my_body_A = std::make_shared<ChBody>();
my_system.AddBody(my_body_A);
my_body_A->SetBodyFixed(true);  // the truss doesn't move
 
// ..the crank
auto my_body_B = std::make_shared<ChBody>();
my_system.AddBody(my_body_B);
my_body_B->SetPos(ChVector<>(1, 0, 0));  // position of COG of crank
my_body_B->SetMass(2);
 
// ..the connecting rod
auto my_body_C = std::make_shared<ChBody>();
my_system.AddBody(my_body_C);
my_body_C->SetPos(ChVector<>(4, 0, 0));  // position of COG of rod
my_body_C->SetMass(3);
 
 
// 3- Create constraints: the mechanical joints 
//    between the rigid bodies.
 
// .. a revolute joint between the crank and rod
auto my_link_BC = std::make_shared<ChLinkLockRevolute>();
my_link_BC->Initialize(my_body_B, my_body_C, ChCoordsys<>(ChVector<>(2, 0, 0)));
my_system.AddLink(my_link_BC);
 
// .. a slider joint between the rod and truss
auto my_link_CA = std::make_shared<ChLinkLockPointLine>();
my_link_CA->Initialize(my_body_C, my_body_A, ChCoordsys<>(ChVector<>(6, 0, 0)));
my_system.AddLink(my_link_CA);
 
// .. an engine (motion generator) between the crank and truss
auto my_link_AB = std::make_shared<ChLinkEngine>();
my_link_AB->Initialize(my_body_A, my_body_B, ChCoordsys<>(ChVector<>(0, 0, 0)));
my_link_AB->Set_eng_mode(ChLinkEngine::ENG_MODE_SPEED);
if (auto mfun = std::dynamic_pointer_cast<ChFunction_Const>(my_link_AB->Get_spe_funct()))
    mfun->Set_yconst(CH_C_PI);  // speed w=3.145 rad/sec
my_system.AddLink(my_link_AB);
    
    
// 4- Adjust settings of the integrator (optional):
my_system.SetIntegrationType(ChSystem::INT_IMPLICIT_EULER)
my_system.SetSolverType(ChSystem::SOLVER_SOR);
my_system.SetMaxItersSolverSpeed(20);
my_system.SetMaxItersSolverStab(20);
my_system.SetMaxPenetrationRecoverySpeed(0.2);
my_system.SetMinBounceSpeed(0.1);
        
// 5- Run the simulation (basic example)
 
while( my_system.GetChTime() < 10 )
{       
    // Chrono advances the state of the system via time integration
    // with a time step of 0.02
    my_system.StepDynamics(0.02);
 
    // Draw items on screen (lines, circles, etc.) or dump data to disk 
    [..] 
}

The default simulation settings are good for real-time fast simulations with low requirements in terms of precision and with similar sizes and inertia attributes.

Several system settings may be adjusted to simulate more challenging scenarios. In most cases there are three areas to adjust:

The time stepper; i.e., the time integration algorithm
The solver; i.e., the algorithm that computes accelerations and reaction forces at each time step
Other settings, for instance, the collision detection tolerances

A primer on tuning these parameters is provided below.

Time steppers

Time steppers, also known as time integrators, are used to advance the simulation. They perform numerical integration; i.e., they advance the state of the system in time.

Technical and theoretical details on time integration are explained in several PDF documents available on the white papers page. For example this PDF explains how implicit integrators are implemented in Chrono.

Time steppers can be changed in two ways:

Using the my_system.SetTimestepperType(...) function, to choose a ready-to-use, pre-packaged time-stepper
Using the my_system.SetTimestepper(...) function, to plug in a custom time-stepper, which is user-defined

Example: changing the time stepper to an implicit numerical integrator

my_system.SetTimestepperType(ChTimestepper::Type::IMPLICIT_EULER)

Summary of time-steppers:

EULER_IMPLICIT_LINEARIZED
- Default time stepper in Chrono
- Fast, no sub-iterations required
- First order accuracy
- Works for DVI contacts (hard contacts)
- Delivers first order accuracy for FEA
- Constraints kept closed using stabilization
HHT
- Implicit integrator, based on the Hilber-Hughes-Taylor formula
- Typically slower than the INT_EULER_IMPLICIT_LINEARIZED choice
- Sub-iterations required
- Second order accuracy, with adjustable numerical damping
- Currently can't be used for systems that handle contacts in a DVI approach; i.e., for hard contacts
- Delivers second order accuracy for FEA
- Constraints kept closed exactly because of inner iterations.
NEWMARK
- Popular in the FEA community, similar properties as INT_HHT
- With the exception of one particular choice of parameters (in which it becomes the trapezoidal integration rule) it delivers first order accuracy
In the above, the meaning of 'first order' or 'second order' accuracy is that the global integration error goes to zero as the value of the time step (or square of the time step for a second order method).

Depending on the type of time-stepper used, there may be different parameters to adjust. Example:

if (auto mystepper = std::dynamic_pointer_cast<ChTimestepperHHT>(my_system.GetTimestepper())) {
    mystepper->SetAlpha(-0.2);
    ...
}

See chrono::ChTimestepper for API details.

Solvers

A solver is called by a time stepper to compute the unknown accelerations and unknown reaction forces at each time step of the simulation. Most often they represent the biggest computational bottleneck of the entire simulation.

Solvers can be changed in two ways:

Using the my_system.SetSolverType(...) function, to choose a ready-to-use, pre-packaged option
Using the my_system.SetSolver(...) function, to plug in a custom time-stepper, which is user-defined

Example:

my_system.SetSolverType(ChSolver::Type::SOR);

We recommend using one of the following iterative solvers:

SOR
- low precision: convergence might stall, especially with odd mass ratios
- supports DVI (hard contacts, with complementarity)
- used most often for small problems, solution accuracy is not particularly important
APGD
- very good convergence, used most often for simulations in which high accuracy in results is desired
- supports DVI (hard contacts, with complementarity)
BARZILAIBORWEIN
- good convergence
- supports DVI (hard contacts, with complementarity)
- similar to APGD, might be more robust when using large mass ratios
MINRES
- good convergence
- supports FEA problems
- does nor support DVI (hard contacts, with complementarity) for the moment.

Most iterative solvers have a default value for the max number of iterations for convergence.

When this number is higher, the solver has the chance to 'try harder', which might lead to longer simulation times
When this value is low, the solver is faster but the solution at the end of the iterative process might be not fully converged

The max. number of iterations can be changed as follows:

// Change the max iterations for the solver

my_system.SetMaxItersSolverSpeed(20);

Depending on the type of integrator used, there may be different parameters to adjust. Advanced settings are not accessible directly from chrono::ChSystem, for instance:

if (auto msolver = std::dynamic_pointer_cast<ChSolverMINRES>(my_system.GetSolver())) {
    msolver->SetDiagonalPreconditioning(true);
}

See chrono::ChSolver for API for further details.

Other parameters

There are many integrator/solver settings that can affect the outcome of a simulation. For instance, see collision tolerances to gain a better understanding of the interplay between the accuracy in the collision detection and robustness of a simulation. We focus below on two important settings related to handling collisions in a simulation in which bodies collide with each other and/or with the ground.

Max. recovery speed

Bodies in contact that interpenetrate for various reasons, e.g., small numerical integration error, inconsistent initial conditions, etc., will not 'escape' this contact violation at a speed faster than this threshold. The recovery speed is in general problem dependent and is controlled by user as shown below.

my_system.SetMaxPenetrationRecoverySpeed(0.2);

Larger values allow a more aggressive correction of the penetration, yet this can lead to scenarios in which bodies in contact pop out fast or in stacking problems the stack becoming jittery, noisy
A small threshold increases the risk that objects sink into one another when integrator precision is low, for instance, when the solver has a small max number of iterations

Min. bounce speed

When objects collide, if their incoming speed is lower than this threshold, a zero restitution coefficient is assumed. This helps to achieve more stable simulations of stacked objects.

my_system.SetMinBounceSpeed(0.1);

A higher value leads to more stable simulations but less physically realistic collisions
Lower values lead to a more physically realistic time evolution but require small integration time steps otherwise objects may keep bounce erratically

Theory

Additional information regarding the time integration strategies implemented in Chrono can be found on the white papers page.

Table of Contents