Description
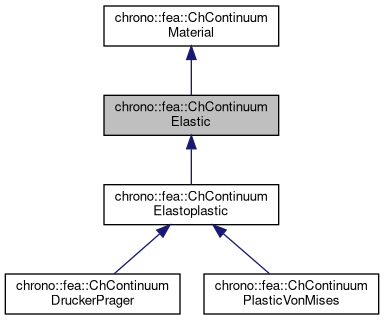
Class for the basic properties of materials in an elastic continuum.
This is a base material with isotropic hookean elasticity.
#include <ChContinuumMaterial.h>
Public Member Functions | |
| ChContinuumElastic (double myoung=10000000, double mpoisson=0.4, double mdensity=1000) | |
| Create a continuum isotropic hookean material. More... | |
| ChContinuumElastic (const ChContinuumElastic &other) | |
| void | Set_E (double m_E) |
| Set the Young E elastic modulus, in Pa (N/m^2), as the ratio of the uniaxial stress over the uniaxial strain, for hookean materials. More... | |
| double | Get_E () const |
| Get the Young E elastic modulus, in Pa (N/m^2). | |
| void | Set_v (double m_v) |
| Set the Poisson v ratio, as v=-transverse_strain/axial_strain, so takes into account the 'squeezing' effect of materials that are pulled (so, if zero, when you push the two sizes of a cube, it won't inflate). More... | |
| double | Get_v () const |
| Get the Young v ratio, as v=-transverse_strain/axial_strain. | |
| void | Set_G (double m_G) |
| Set the shear modulus G, in Pa (N/m^2), as the ratio of shear stress to the shear strain. More... | |
| double | Get_G () const |
| Get the shear modulus G, in Pa (N/m^2) | |
| double | Get_l () const |
| Get Lamé first parameter (the second is shear modulus, so Get_G() ) | |
| double | Get_BulkModulus () const |
| Get bulk modulus (increase of pressure for decrease of volume), in Pa. | |
| double | Get_WaveModulus () const |
| Get P-wave modulus (if V=speed of propagation of a P-wave, then (M/density)=V^2 ) | |
| void | ComputeStressStrainMatrix () |
| Computes Elasticity matrix and stores the value in this->StressStrainMatrix Note: is performed every time you change a material parameter. | |
| ChMatrixDynamic & | Get_StressStrainMatrix () |
| Get the Elasticity matrix. | |
| void | ComputeElasticStress (ChStressTensor<> &mstress, const ChStrainTensor<> &mstrain) const |
| Compute elastic stress from elastic strain (using column tensors, in Voight notation) | |
| void | ComputeElasticStrain (ChStrainTensor<> &mstrain, const ChStressTensor<> &mstress) const |
| Compute elastic strain from elastic stress (using column tensors, in Voight notation) | |
| void | Set_RayleighDampingM (double m_d) |
| Set the Rayleigh mass-proportional damping factor alpha, to build damping R as R=alpha*M + beta*K. | |
| double | Get_RayleighDampingM () const |
| Set the Rayleigh mass-proportional damping factor alpha, in R=alpha*M + beta*K. | |
| void | Set_RayleighDampingK (double m_d) |
| Set the Rayleigh stiffness-proportional damping factor beta, to build damping R as R=alpha*M + beta*K. | |
| double | Get_RayleighDampingK () const |
| Set the Rayleigh stiffness-proportional damping factor beta, in R=alpha*M + beta*K. | |
| virtual void | ArchiveOUT (ChArchiveOut &marchive) override |
| virtual void | ArchiveIN (ChArchiveIn &marchive) override |
 Public Member Functions inherited from chrono::fea::ChContinuumMaterial Public Member Functions inherited from chrono::fea::ChContinuumMaterial | |
| ChContinuumMaterial (double mdensity=1000) | |
| ChContinuumMaterial (const ChContinuumMaterial &other) | |
| void | Set_density (double m_density) |
| Set the density of the material, in kg/m^2. | |
| double | Get_density () const |
| Get the density of the material, in kg/m^2. | |
Additional Inherited Members | |
 Protected Attributes inherited from chrono::fea::ChContinuumMaterial Protected Attributes inherited from chrono::fea::ChContinuumMaterial | |
| double | density |
Constructor & Destructor Documentation
◆ ChContinuumElastic()
| chrono::fea::ChContinuumElastic::ChContinuumElastic | ( | double | myoung = 10000000, |
| double | mpoisson = 0.4, |
||
| double | mdensity = 1000 |
||
| ) |
Create a continuum isotropic hookean material.
Default value for Young elastic modulus is low (like a rubber-type material), and same for density.
Member Function Documentation
◆ Set_E()
| void chrono::fea::ChContinuumElastic::Set_E | ( | double | m_E | ) |
Set the Young E elastic modulus, in Pa (N/m^2), as the ratio of the uniaxial stress over the uniaxial strain, for hookean materials.
Intuitively, the tensile pressure on a side of a parallelepiped in order to double its length. Note that most metal materials require very high values, ex. steel has E=210GPa (E=210e9), aluminium E=69e9, and this can cause numerical problems if you do not set up the simulation integrator properly.
◆ Set_G()
| void chrono::fea::ChContinuumElastic::Set_G | ( | double | m_G | ) |
Set the shear modulus G, in Pa (N/m^2), as the ratio of shear stress to the shear strain.
Setting G also changes Poisson ratio v.
◆ Set_v()
| void chrono::fea::ChContinuumElastic::Set_v | ( | double | m_v | ) |
Set the Poisson v ratio, as v=-transverse_strain/axial_strain, so takes into account the 'squeezing' effect of materials that are pulled (so, if zero, when you push the two sizes of a cube, it won't inflate).
Most materials have some 0<v<0.5, for example steel has v=0.27..0.30, aluminium v=0.33, rubber=0.49, etc. Note! v=0.5 means perfectly incompressible material, that could give problems with some type of solvers. Setting v also changes G.
The documentation for this class was generated from the following files:
- /builds/uwsbel/chrono/src/chrono/fea/ChContinuumMaterial.h
- /builds/uwsbel/chrono/src/chrono/fea/ChContinuumMaterial.cpp
