Table of Contents
- ChElementSpring
- ChElementBar
- ChElementTetraCorot_4
- ChElementTetraCorot_10
- ChElementHexaCorot_8
- ChElementHexaCorot_20
- ChElementHexaANCF_3813
- ChElementHexaANCF_3813_9
- ChElementHexaANCF_3843
- ChElementCableANCF
- ChElementBeamANCF_3243
- ChElementBeamANCF_3333
- ChElementBeamEuler
- ChElementBeamIGA
- ChElementShellReissner
- ChElementShellANCF_3423
- ChElementShellANCF_3443
- ChElementShellANCF_3833
- ChElementShellBST
Different types of finite elements can be used in the FEA module. In this page you can find a description of their properties.
- An element connects N nodes.
- Nodes are handled via std::shared_ptr shared pointers: you do not have to worry about deleting them.
- Add elements to a mesh using ChMesh::AddElement()
- Initialize the elements by telling which node are connected with SetNodes()
- Set a material property to the element by using SetMaterial()
ChElementSpring

The chrono::fea::ChElementSpring is the simplest element, and it can be used as a starting point to learn how to implement finite elements.
Moreover, it is useful for problems like trusses, suspensions, etc. this base implementation This spring assumes linear behavior, but experienced programmers can override this class and implement more advanced non-linear spring models.
- 2 nodes of ChNodeFEAxyz type
- Large displacements allowed
- Zero mass element
- Parameters:
- rest length L,
- stiffness k,
- damping r
- Stiffness matrix computed analytically for high performance (both material and geometric stiffness are supported).
ChElementBar
The chrono::fea::ChElementBar is quite similar to the ChElementSpring, but adds the effect of mass, and uses different parameters at construction time.
- 2 nodes of ChNodeFEAxyz type
- Very similar to ChElementSpring, except it has a mass
- No torque at the ends (like two spherical joints)
- Large displacements allowed
- Parameters:
- rest length L,
- Section area A,
- Young modulus E,
- damping (like in Rayleight beta parameter)
- Stiffness matrix computed analytically for high performance (both material and geometric stiffness are supported).
ChElementTetraCorot_4
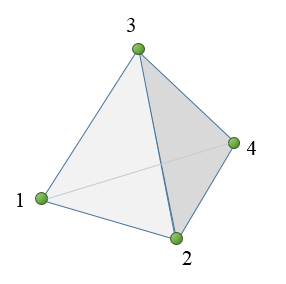
The chrono::fea::ChElementTetraCorot_4 is the simplest volume element for simulating 3D problems.
- 4 nodes of ChNodeFEAxyz type
- Linear interpolation, constant stress
- 1 integration point
- Corotational formulation for large displacements
- Uses polar decomposition for corotated frame
- Useful for solids
- Fastest element for solids
- Stiffness matrix computed analytically for high performance (note, geometric stiffness term not added at the moment).
ChElementTetraCorot_10
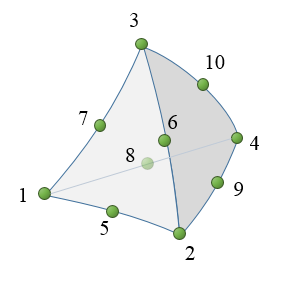
The chrono::fea::ChElementTetraCorot_10 is a quadratic volume element based on tetahedrons with intermediate nodes along edges, as in figure.
- 10 nodes of ChNodeFEAxyz type
- Quadratic interpolation, linear stress
- 4 integration points
- Corotational formulation for large displacements
- Uses polar decomposition for corotated frame
- Note: initial position assuming nodes n>4 exactly at mid-length of edges
- Useful for solids
- Stiffness matrix computed analytically for high performance (note, geometric stiffness term not added at the moment).
ChElementHexaCorot_8
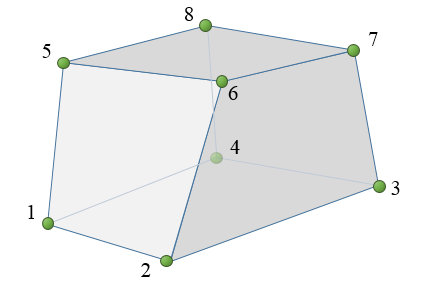
The chrono::fea::ChElementHexaCorot_8 is a linear isoparametric element of brick type.
- 8 nodes of ChNodeFEAxyz type
- Linear interpolation
- 8 integration points
- Corotational formulation for large displacements
- Useful for solids, with structured grids
- Stiffness matrix computed analytically for high performance (note, geometric stiffness term not added at the moment).
ChElementHexaCorot_20
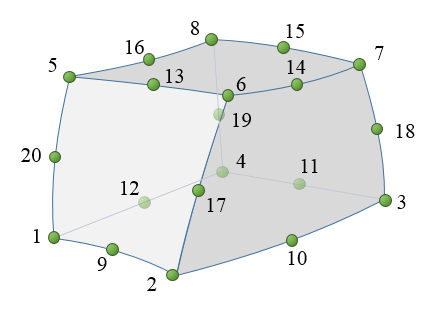
The chrono::fea::ChElementHexaCorot_20 is a quadratic isoparametric element of brick type.
- 20 nodes of ChNodeFEAxyz type
- 8 at vertexes, 12 at edges midpoints
- Quadratic interpolation
- 27 integration points
- Corotational formulation for large displacements
- Useful for solids, with structured grids
- Stiffness matrix computed analytically for high performance (note, geometric stiffness term not added at the moment).
ChElementHexaANCF_3813

The chrono::fea::ChElementHexaANCF_3813 is a brick element implemented using the ANCF formulation.
- 8 nodes of ChNodeFEAxyz type
- Linear interpolation
- 8 integration points
- Use EAS Enhanced Assumed Strain
- Large strains
- Can use Mooney-Rivlin model for hyperelastic materials
- Useful for solids, with structured grids
ChElementHexaANCF_3813_9
The chrono::fea::ChElementHexaANCF_3813_9 is a brick element implemented using the ANCF formulation.
- 9 nodes of ChNodeFEAxyz type (8 at the corners, 1 at the center)
- Linear interpolation
- 8 integration points
- Strain formulations for large strains:
- Green-Lagrange
- Hencky
- Plasticity:
- J2 (metals)
- DruckerPrager (soil, plastics)
- DruckerPrager_Cap (soil, plastics)
- Useful for solids, with structured grids
ChElementHexaANCF_3843
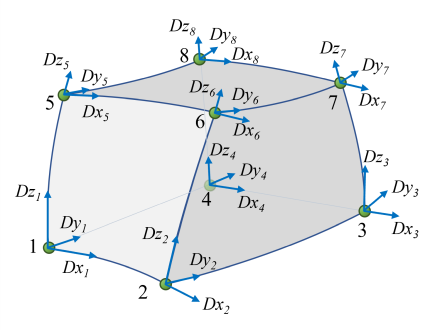
The chrono::fea::ChElementHexaANCF_3843 is a 8 node brick element based on the ANCF approach with a full set of position vector gradient coordinates at each node.
- 8 nodes of ChNodeFEAxyzDDD type
- 64 integration points
- ANCF formulation for large displacements
- Useful for solids, with structured grids
ChElementCableANCF
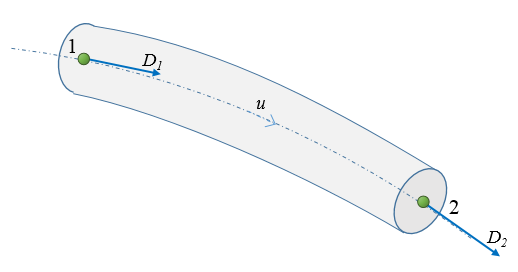
The chrono::fea::ChElementCableANCF is a fast element for the simulation of thin beams (cables, wires, ropes) where one is not interested in twisting, shear, etc.
- 2 nodes of chrono::fea::ChNodeFEAxyzD type
- 3 integration point (stiffness), 4 (mass)
- ANCF formulation for large displacements
- Thin beam (no shear)
- Does not model torsional stiffness (useful for wires, cables)
- Section property: A, I, E, density, damping, defined via a chrono::fea::ChBeamSectionCable object.
ChElementBeamANCF_3243
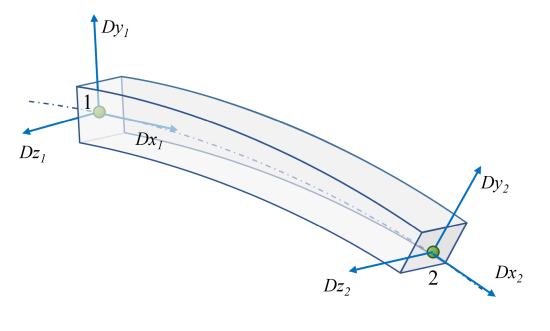
The chrono::fea::ChElementBeamANCF_3243 is a thick beam element implemented using the ANCF formulation with a full set of position vector gradient coordinates at each node. As an alternative, we also provide a chrono::fea::ChElementBeamIGA with more advanced functionality in the field of Geometrically Exact Beam theory.
- 2 nodes of chrono::fea::ChNodeFEAxyzDDD type
- ANCF formulation for large displacements
- Section property: rectangular width-height, E, Poisson ratio, shear correction factors, density
ChElementBeamANCF_3333
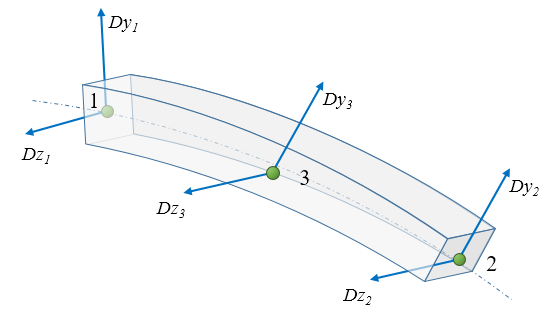
The chrono::fea::ChElementBeamANCF_3333 is a thick beam element implemented using the ANCF formulation. As an alternative, we also provide a chrono::fea::ChElementBeamIGA with more advanced functionality in the field of Geometrically Exact Beam theory.
- 3 nodes of chrono::fea::ChNodeFEAxyzDD type
- ANCF formulation for large displacements
- Section property: rectangular width-height, E, Poisson ratio, shear correction factors, density
ChElementBeamEuler

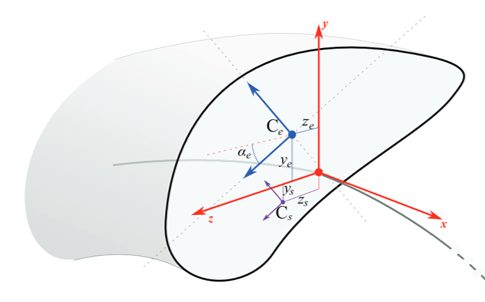
The chrono::fea::ChElementBeamEuler is a thin beam element, using the corotated Euler-Bernoulli theory in 3D. For low/moderate bending, and if shear effects are not important (thin beam assumption), this formulation is very efficient.
- 2 nodes of chrono::fea::ChNodeFEAxyzrot type
- Linear interpolation
- 1 integration point (default)
- Corotational formulation for large displacements
- Thin beam (no shear), based on the Euler-Bernoulli thin beam theory
- Section properties include settings for:
- A, A, Iyy, Izz, (or axial and bending rigidity),
- G, J (or torsional rigidity),
- density, damping plus optional:
- αe , ze , ye , for offset/rotated section
- zs , ys for offset shear center
- The section properties are defined via chrono::fea::ChBeamSectionEuler classes, among these:
- chrono::fea::ChBeamSectionEulerSimple , for uniform elasticity, uniform density
- chrono::fea::ChBeamSectionEulerAdvanced , as above, adds offset/rotated section and shear center
- chrono::fea::ChBeamSectionEulerAdvancedGeneric , if non-uniform elasticity or non-uniform density
- chrono::fea::ChBeamSectionEulerEasyCircular , an easy-to-use shortcut
- chrono::fea::ChBeamSectionEulerEasyRectangular , an easy-to-use shortcut
- both material and geometric stiffness are computed.
ChElementBeamIGA
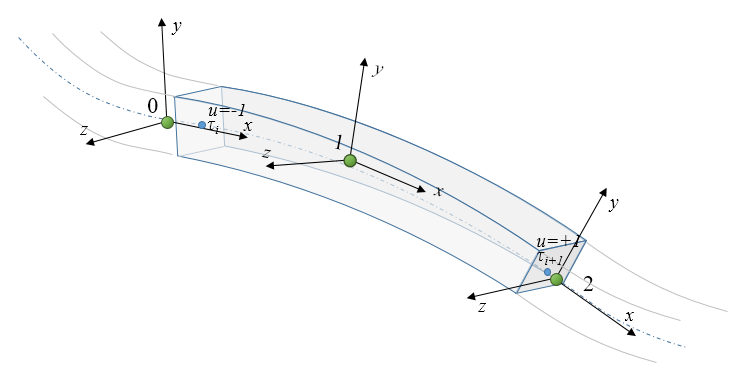
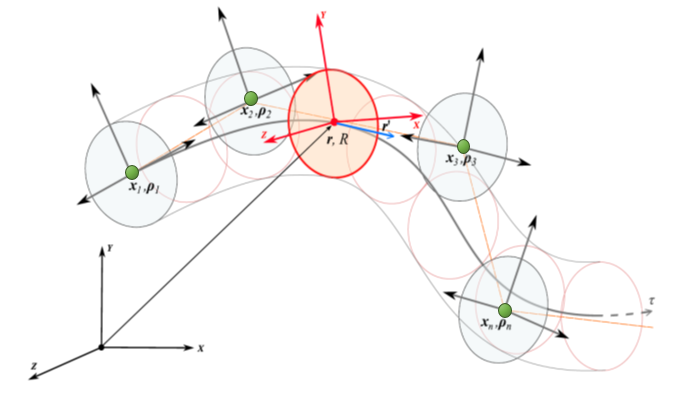
The chrono::fea::ChElementBeamIGA is a thick beam element based on the Isogeometric Analysis (IGA) hence with a B-Spline shape, and relying on the Geometrically Exact Beam theory.
- Isogeometric formulation (IGA) of a Cosserat rod, with large displacements
- User-defined order n (ex: 1=linear 2=quadratic, 3=cubic).
- Each element is a span of a b-spline, so each element uses n+1 control points, ie. nodes of chrono::fea::ChNodeFEAxyzrot type
- Thick beam shear effects are possible, v. Timoshenko theory
- Reduced integration to correct shear locking
- Initial curved configuration is supported
- Suggestion: use ChBuilderBeamIGA for easy creation a full B-spine, ie. given full knot sequence and points as in the second figure above.
- Section defined in a modular way, via a chrono::fea::ChBeamSectionCosserat that is composed via
- Elasticity model from chrono::fea::ChElasticityCosserat, ex:
- Inertial model from chrono::fea::ChInertiaCosserat, ex:
- Damping model from chrono::fea::ChDampingCosserat (optional), ex:
- Plasticity model from chrono::fea::ChPlastcityCosserat (optional)
- Some of the sectional properties above support the case of offsets in center of mass, center of shear, center of axial elastic forces, as well as rotation of the section axes, for defining complex beams like helicopter blades
- Both material and geometric stiffness are considered.
ChElementShellReissner
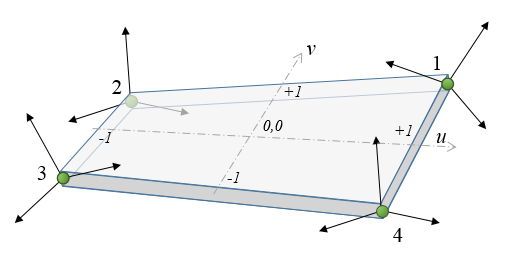
The chrono::fea::ChElementShellReissner is a quadrilateral thick shell element.
- 4 nodes of chrono::fea::ChNodeFEAxyzrot type
- Bi-linear interpolation
- 4 integration points (default)
- Allows large displacements, exponential map used for SO3
- Thick shells allowed
- Based on the Reissner 6-field shell theory (w. drilling stiffness)
- Can have multi-layered materials, using CLT thory
- ANS, shear-lock free
- Nodes need not to be aligned to shell (rotation offsets auto-computed in initialization)
- Section defined in a modular way, via N layers, each with a chrono::fea::ChMaterialShellReissner composed by:
- Elasticity model from chrono::fea::ChElasticityReissner, ex:
- Damping model from chrono::fea::ChDampingReissner (optional)
- Plasticity model from chrono::fea::ChPlasticityReissner (optional)
ChElementShellANCF_3423
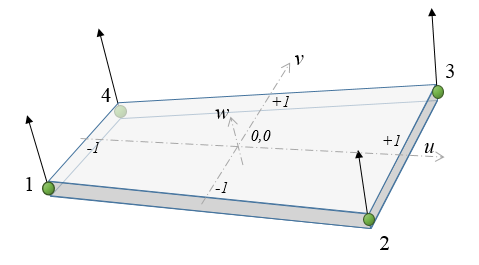
The chrono::fea::ChElementShellANCF_3423 is a quadrilateral thick shell element based on the ANCF approach.
- 4 nodes of chrono::fea::ChNodeFEAxyzD type
- Bi-linear interpolation
- 4 integration points (default)
- Allows large displacements, using ANCF formulation
- Thick shells allowed
- Can have multi-layered materials
- ANS-EAS, shear-lock free
- Nodes D must be aligned to shell normal at initialization
ChElementShellANCF_3443
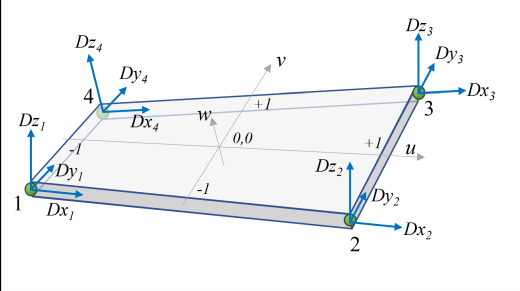
The chrono::fea::ChElementShellANCF_3443 is a quadrilateral thick shell element based on the ANCF approach with a full set of position vector gradient coordinates at each node.
- 4 nodes of chrono::fea::ChNodeFEAxyzDDD type
- Allows large displacements, using ANCF formulation
- Thick shells allowed
- Can have multi-layered materials
- Locking is a concern with this element as it is currently formulated
ChElementShellANCF_3833
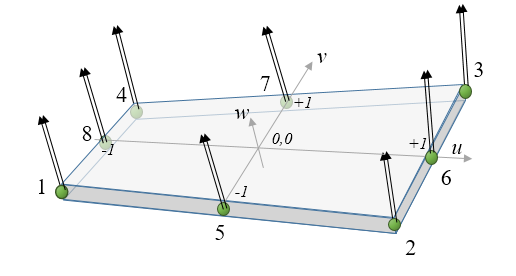
The chrono::fea::ChElementShellANCF_3833 is a quadrilateral thick shell element based on the ANCF approach.
- 8 nodes of chrono::fea::ChNodeFEAxyzDD type
- Higher order interpolation
- Allows large displacements, using ANCF formulation
- Thick shells allowed
- Can have multi-layered materials
- Formulated to be shear-lock free
- Nodes D must be aligned to shell normal at initialization
ChElementShellBST
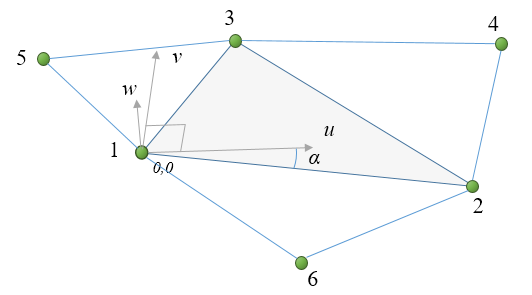
The chrono::fea::ChElementShellBST is a triangular thin shell element that offers very high computational efficiency.
- Triangular thin-shell
- 6 nodes of chrono::fea::ChNodeFEAxyz type
- 1,2,3 from the triangle
- 4,5,6 from the neighbouring triangles (any can be optional if on the boundary)
- Constant strain, constant curvature computed from bent triangle neighbours
- Allows large deformation
- Can have multi-layered materials
- Based on Kirchhoff-Love theory (no shear), good for tissues, sails, etc.
- Section defined in a modular way, via N layers, each with a chrono::fea::ChMaterialShellKirchhoff composed by:
- Elasticity model from chrono::fea::ChElasticityKirchhoff, ex:
- Damping model from chrono::fea::ChDampingKirchhoff (optional)
- Plasticity model from chrono::fea::ChPlasticityKirchhoff (optional)
Theory
Additional information regarding the implementation of finite elements in Chrono can be found at the
whitepapers page.
Examples
See demos and examples at the tutorials page.
