Description
Solves the eigenvalue problem with the Krylov-Schur iterative method.
This is an efficient method to compute only the lower n modes, ex. when there are so many degreees of freedom that it would make a full solution impossible. It uses an iterative method and it exploits the sparsity of the matrices.
#include <ChEigenvalueSolver.h>
Public Member Functions | |
| ChQuadraticEigenvalueSolverKrylovSchur (ChDirectSolverLScomplex *mlinear_solver=0) | |
| Default: uses Eigen::SparseQR as factorization for the shift&invert, otherwise pass a custom complex sparse solver for faster factorization (ex. More... | |
| virtual bool | Solve (const ChSparseMatrix &M, const ChSparseMatrix &R, const ChSparseMatrix &K, const ChSparseMatrix &Cq, ChMatrixDynamic< std::complex< double >> &eigvects, ChVectorDynamic< std::complex< double >> &eigvals, ChVectorDynamic< double > &freq, ChVectorDynamic< double > &damping_ratio, ChEigenvalueSolverSettings settings=0) const override |
| Solve the quadratic eigenvalue problem (lambda^2*M + lambda*R + K)*x = 0 s.t. More... | |
| virtual bool | Solve (ChAssembly &assembly, ChMatrixDynamic< std::complex< double >> &eigvects, ChVectorDynamic< std::complex< double >> &eigvals, ChVectorDynamic< double > &freq, ChVectorDynamic< double > &damping_ratio, ChEigenvalueSolverSettings settings=0) const override |
| Solve the quadratic eigenvalue problem (lambda^2*M + lambda*R + K)*x = 0 s.t. More... | |
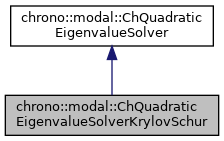
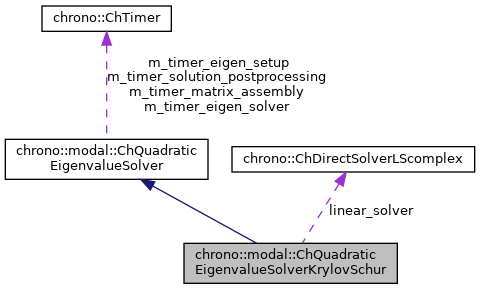
 Public Member Functions inherited from chrono::modal::ChQuadraticEigenvalueSolver Public Member Functions inherited from chrono::modal::ChQuadraticEigenvalueSolver | |
| double | GetTimeMatrixAssembly () const |
| Get cumulative time for matrix assembly. | |
| double | GetTimeEigenSetup () const |
| Get cumulative time eigensolver setup. | |
| double | GetTimeEigenSolver () const |
| Get cumulative time eigensolver solution. | |
| double | GetTimeSolutionPostProcessing () const |
| Get cumulative time for post-solver solution postprocessing. | |
Public Attributes | |
| ChDirectSolverLScomplex * | linear_solver |
Additional Inherited Members | |
 Protected Attributes inherited from chrono::modal::ChQuadraticEigenvalueSolver Protected Attributes inherited from chrono::modal::ChQuadraticEigenvalueSolver | |
| ChTimer | m_timer_matrix_assembly |
| timer for matrix assembly | |
| ChTimer | m_timer_eigen_setup |
| timer for eigensolver setup | |
| ChTimer | m_timer_eigen_solver |
| timer for eigensolver solution | |
| ChTimer | m_timer_solution_postprocessing |
| timer for conversion of eigensolver solution | |
Constructor & Destructor Documentation
◆ ChQuadraticEigenvalueSolverKrylovSchur()
| chrono::modal::ChQuadraticEigenvalueSolverKrylovSchur::ChQuadraticEigenvalueSolverKrylovSchur | ( | ChDirectSolverLScomplex * | mlinear_solver = 0 | ) |
Default: uses Eigen::SparseQR as factorization for the shift&invert, otherwise pass a custom complex sparse solver for faster factorization (ex.
Member Function Documentation
◆ Solve() [1/2]
|
overridevirtual |
Solve the quadratic eigenvalue problem (lambda^2*M + lambda*R + K)*x = 0 s.t.
Cq*x = 0 If n_modes=0, return all eigenvalues, otherwise only the first lower n_modes.
< output matrix with eigenvectors as columns, will be resized
< output vector with eigenvalues (real part not zero if some damping), will be resized
< 0 = k-th eigenvalue is real, 1= k-th and k-th+1 are complex conjugate pairs
< 0 = has converged, 1 = hasn't converged
< number of converged eigenvalues
< number of used iterations
< callback for A*v
< initial approx of eigenvector, or random
< size of A
< number of needed eigenvalues
< Krylov restart threshold (largest dimension of krylov subspace)
< max iteration number
< tolerance
- Parameters
-
assembly assembly on which to apply the eigen solver eigvects output matrix with eigenvectors as columns, will be resized eigvals output vector with eigenvalues (real part not zero if some damping), will be resized freq output vector with n undamped frequencies [Hz], as f=w/(2*PI), will be resized. damping_ratio output vector with n damping rations r=damping/critical_damping. settings optional: settings for the solver, or n. of desired lower eigenvalues. If =0, return all eigenvalues.
Implements chrono::modal::ChQuadraticEigenvalueSolver.
◆ Solve() [2/2]
|
overridevirtual |
Solve the quadratic eigenvalue problem (lambda^2*M + lambda*R + K)*x = 0 s.t.
Cq*x = 0 Returns only the first lower n_modes. If n_modes=0, it return all eigenvalues (performance warning)
< output matrix with eigenvectors as columns, will be resized
< output vector with eigenvalues (real part not zero if some damping), will be resized
< 0 = k-th eigenvalue is real, 1= k-th and k-th+1 are complex conjugate pairs
< 0 = has converged, 1 = hasn't converged
< number of converged eigenvalues
< number of used iterations
< callback for A*v
< initial approx of eigenvector, or random
< size of A
< number of needed eigenvalues
< Krylov restart threshold (largest dimension of krylov subspace)
< max iteration number
< tolerance
- Parameters
-
M input M matrix R input R matrix K input K matrix Cq input Cq matrix of constraint jacobians eigvects output matrix with eigenvectors as columns, will be resized eigvals output vector with complex eigenvalues (real part not zero if some damping), will be resized freq output vector with n frequencies [Hz], as f=w/(2*PI), will be resized. damping_ratio output vector with n damping rations r=damping/critical_damping. settings optional: settings for the solver, or n. of desired lower eigenvalues.
Implements chrono::modal::ChQuadraticEigenvalueSolver.
The documentation for this class was generated from the following files:
- /builds/uwsbel/chrono/src/chrono_modal/ChEigenvalueSolver.h
- /builds/uwsbel/chrono/src/chrono_modal/ChEigenvalueSolver.cpp
