Description
Solves the eigenvalue problem with the Krylov-Schur iterative method.
This is an efficient method to compute only the lower n modes, ex. when there are so many degreees of freedom that it would make a full solution impossible. It uses an iterative method and it exploits the sparsity of the matrices.
#include <ChEigenvalueSolver.h>
Public Member Functions | |
| ChQuadraticEigenvalueSolverKrylovSchur (ChDirectSolverLScomplex *mlinear_solver=0) | |
| Default: uses Eigen::SparseQR as factorization for the shift&invert, otherwise pass a custom complex sparse solver for faster factorization (ex. More... | |
| virtual bool | Solve (const ChSparseMatrix &M, const ChSparseMatrix &R, const ChSparseMatrix &K, const ChSparseMatrix &Cq, ChMatrixDynamic< std::complex< double >> &V, ChVectorDynamic< std::complex< double >> &eig, ChVectorDynamic< double > &freq, ChVectorDynamic< double > &damping_ratio, ChEigenvalueSolverSettings settings=0) const override |
| Solve the quadratic eigenvalue problem (lambda^2*M + lambda*R + K)*x = 0 s.t. More... | |
Public Attributes | |
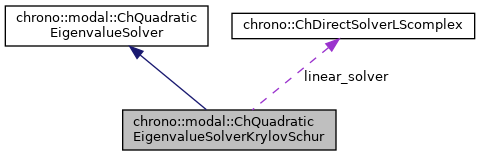
| ChDirectSolverLScomplex * | linear_solver |
Constructor & Destructor Documentation
◆ ChQuadraticEigenvalueSolverKrylovSchur()
| chrono::modal::ChQuadraticEigenvalueSolverKrylovSchur::ChQuadraticEigenvalueSolverKrylovSchur | ( | ChDirectSolverLScomplex * | mlinear_solver = 0 | ) |
Default: uses Eigen::SparseQR as factorization for the shift&invert, otherwise pass a custom complex sparse solver for faster factorization (ex.
Member Function Documentation
◆ Solve()
|
overridevirtual |
Solve the quadratic eigenvalue problem (lambda^2*M + lambda*R + K)*x = 0 s.t.
Cq*x = 0 Returns only the first lower n_modes. If n_modes=0, it return all eigenvalues (performance warning)
< output matrix with eigenvectors as columns, will be resized
< output vector with eigenvalues (real part not zero if some damping), will be resized
< 0 = k-th eigenvalue is real, 1= k-th and k-th+1 are complex conjugate pairs
< 0 = has converged, 1 = hasn't converged
< number of converged eigenvalues
< number of used iterations
< callback for A*v
< initial approx of eigenvector, or random
< size of A
< number of needed eigenvalues
< Krylov restart threshold (largest dimension of krylov subspace)
< max iteration number
< tolerance
- Parameters
-
M input M matrix R input R matrix K input K matrix Cq input Cq matrix of constraint jacobians V output matrix with eigenvectors as columns, will be resized eig output vector with complex eigenvalues (real part not zero if some damping), will be resized freq output vector with n frequencies [Hz], as f=w/(2*PI), will be resized. damping_ratio output vector with n damping rations r=damping/critical_damping. settings optional: settings for the solver, or n. of desired lower eigenvalues.
Implements chrono::modal::ChQuadraticEigenvalueSolver.
The documentation for this class was generated from the following files:
- /builds/uwsbel/chrono/src/chrono_modal/ChEigenvalueSolver.h
- /builds/uwsbel/chrono/src/chrono_modal/ChEigenvalueSolver.cpp
