Table of Contents
Translation and rotations, together with their transformations, are key elements in the Chrono library.
While translations in the 3D space are exclusively expressed as vectors, the user might encounter either quaternions or, more rarely, rotation matrices to represent rotations (usually for performance reasons).
The recommendation is to rely on quaternions wherever possible and to leverage the appropriate conversions to rotations matrices if required.
Chrono relies on different objects to represents coordinate systems (ChCoordsys, ChFrame, ChFrameMoving, ChMarker, ...) in order to leverage different features and optimizations.
However, the user is usually requested to deal with ChCoordsys or ChFrame only, on which we recommend the beginner user to focus on.
Some basic knowledge of the overall structure might help to better handle these objects:
- ChCoordsys and ChFrame are the most important base classes;
- ChCoordsys is the most basic object, consisting in just a pair of
ChVector3plus aChQuaternion; - ChFrame is the most used throughout Chrono; it embeds a
ChCoordsysand just adds a rotation matrix to improve the performance; - both ChCoordsys and ChFrame easily allow all kind of transformations and change of coordinates at the position level (translation and rotation);
- ChFrameMoving adds transformations at the velocity and acceleration levels;
- ChMarker offers similar capabilities to
ChFrameMovingbut it is attached to a body and follows it during motion;
All the classes discussed in this page are templated in order to hold different scalar types. However, in order to have a cleaner code, some specialization for double and float and sometimes int types are offered. Their names follow the pattern ClassName[d|f|i].
Vectors
Vectors that represent 3D points in space are defined by means of the ChVector3 class.
In mathematical notation:
\[ \mathbf{p}=\{p_x, p_y, p_z\} \]
Construction
The general construction of ChVector3s is through its constructor
However, Chrono offers also a useful set of constant (double) vectors - VNULL, VECT_X, VECT_Y, VECT_Z - that represent the null and the axes unit vectors, respectively.
Usage
ChVector3s hold three coefficients, accessible through chrono::ChVector3<>::x(), y() or z().
Since ChVector3 does not inherit from Eigen vectors it is required to apply a conversion through .eigen() to leverage Eigen capabilities.
ChVectors can be modified and used through:
- their methods, as defined in the class interface; including all the overloaded operators
+,-,*, etc. - free functions, starting with the
Vuppercase letter,Vcross
Quaternions
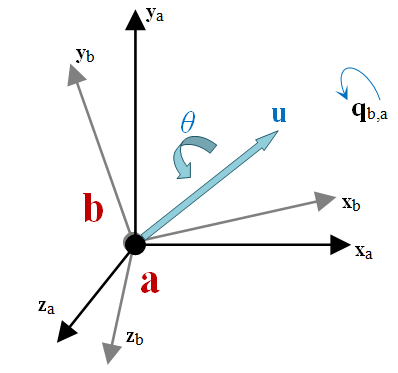
Rotations in Chrono are mainly described by quaternions, as implemented in the ChQuaternion class, according to the axis-angle pair representation:
\[ \mathbf{q}=\left\{ \begin{array}{c} q_0\\ q_1\\ q_2\\ q_3 \end{array} \right\}=\left\{ \begin{array}{c} \cos(\theta / 2)\\ {u}_x \sin(\theta / 2)\\ {u}_y \sin(\theta / 2)\\ {u}_z \sin(\theta / 2) \end{array} \right\} \]
in which should be noted that the scalar part is at the first position.
Given the template nature of the class, it is required to specify the scalar type; however, useful predefined specializations are offered, e.g. ChQuaterniond for the double type.
Please remember that:
- only unit-norm quaternions represent valid rotations;
- the neutral quaternion QUNIT, representing no rotation, is defined by quadruplet
(1, 0, 0, 0).
Construction
Quaternions can be built by explicitly providing their components in the constructor, e.g.
but in many cases it is convenient to build from:
QuatFrom___free functions, defined in ChRotation.h.
e.g. QuatFromAngleAxis or QuatFromAngleY- predefined quaternion, defined in ChQuaternion.h.
e.g.Q_ROTATE_Z_TO_Xor QUNIT
Usage
The ChQuaternion class allows to apply rotations on other items, being them ChVector3, ChFrame or other ChQuaternions as well.
The rotation of a point by a quaternion can be easily done by using the .Rotate() member function. The example below shows how to rotate a point by 20 degrees about the Y axis:
The * operator is used to perform the quaternion (Hamilton) product. From a kinematic perspective, this represents concatenation of rotations. For example, a rotation qA followed by a rotation qB can be condensed in a single rotation qC by pre-multiplication, as follows:
Alternatively, for convenience, the >> operator can be used to achieve the same result, but writing items from left to right:
Rotation matrices
As an alternative to quaternions, Chrono offers the use of 3x3 rotation matrices \( \mathbf{R} \in \mathsf{SO}(3) \) to describe the orientation of a reference frame with respect to another (consult chrono::ChMatrix33 for specific information). Note that a rotation matrix is orthonormal, therefore \( \mathbf{R}^{-1} = \mathbf{R}^{T} \).
Several methods are available for the creation of a rotation matrix and its conversion to other representations. The example below illustrates some construction options:
The * operator can be used to multiply two rotation matrices. For instance, a rotation rotmA followed by a rotation rotmB is given by:
The * operator can also be used to multiply a ChVector3d; this corresponds to rotating the vector:
ChCoordsys
A chrono::ChCoordsys represents a coordinate system in 3D space. It embeds both a vector (coordinate translation \( \mathbf{d} \) ) and a quaternion (coordinate rotation \( \mathbf{q} \) ):
\[ \mathbf{c}=\{\mathbf{d},\mathbf{q}\} \]
The ChCoordys is a lightweight version of a ChFrame, which is discussed next.
ChFrame
A chrono::ChFrame represents a coordinate system in 3D space like ChCoordsys, but it includes more advanced features.
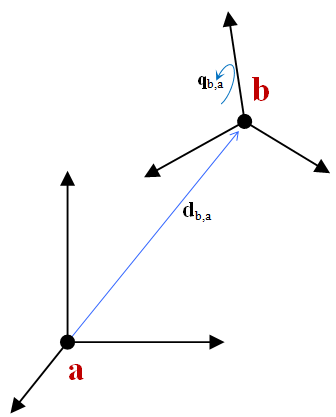
As shown in the picture above, a ChFrame object indicates how "rotated" and "displaced" a coordinate system b is with respect to another coordinate system a. Many time a is the absolute reference frame.
\[ \mathbf{d}_{a,b(c)} \]
is used to define a vector \( \mathbf{d} \) ending in point \( a \), starting from point \( b \), expressed in the base \( c \) (that is, measured along the x,y,z axes of the coordinate system \( c \) ). If \( b \) is omitted, it is assumed to be the origin of the absolute reference frame.As a ChCoordsys, a ChFrame object has a vector for the translation and a quaternion for the rotation:
\[ \mathbf{c}=\{\mathbf{d},\mathbf{q}\} \]
However, the ChFrame class also stores an auxiliary 3x3 rotation matrix that can be used to speed up computations in the cases where quaternions would be less efficient. In this sense, ChCoordsys can be considered as a lightweight version of ChFrame, that may save memory if advanced features are not needed.
Construction
There are several ways to build a ChFrame; for instance:
Usage
One of the most important features of the ChFrame class is the ability to apply coordinate transformations to:
- directions: the transformation is applied to a vector describing a direction: the vector is only rotated but no offset is applied due to the different location of the origin of the new reference system;
\[ \mathbf{d}_{P,a(a)}=\mathbf{R}_{ba} \mathbf{d}_{P,b(b)} \]
The related methods are ChFrame<>::TransformDirectionLocalToParent() and ChFrame<>::TransformDirectionParentToLocal(); - locations: the transformation is applied to a vector describing a location: when transformed, the vector is rotated and the different location of the new reference system is taken into consideration
\[ \mathbf{d}_{P,a(a)}=\mathbf{d}_{b,a(a)} + \mathbf{R}_{ba} \mathbf{d}_{P,b(b)} \]
The related functions are ChFrame<>::TransformPointLocalToParent() and ChFrame<>::TransformPointParentToLocal(); - wrenches transformation: the transformation is applied to a wrench i.e. a pair of a force and a torque: a force expressed in a different reference system lead to an additional torque component, simply due to the change of frame.
The related methods are ChFrame<>::TransformWrenchLocalToParent() and ChFrame<>::TransformWrenchParentToLocal().
Direction and location transformations are by far the most used features thus being worth further details. As example, we can consider the transformation of a point expressed in a local coordinate system b into another (e.g. absolute) coordinate system a:
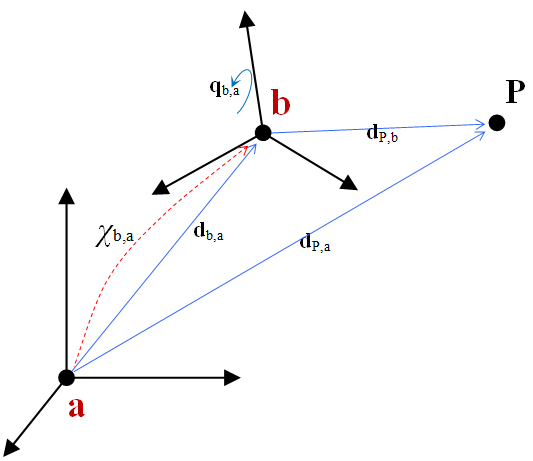
This affine transformation can be written as:
\[ \mathbf{d}_{P,a(a)}=\mathbf{d}_{b,a(a)} + \mathbf{R}_{ba} \mathbf{d}_{P,b(b)} \]
In Chrono, this process can be expressed, without using ChFrame<>s as:
On the contrary, by using ChFrame<> methods, it is possible to simplify the notation, by leveraging one of these three similar approaches:
- using
Transform[Direction|Point]ParentToLocal|Transform[Direction|Point]LocalToParent; more verbose, standard approach - using the
*operator;ChVector3d d_Pa_a; // vector with endpoint P, starting from point a, expressed in frame (a)ChVector3d d_Pb_b; // vector with endpoint P, starting from point b, expressed in frame (b)ChFramed X_ba; // frame (b) (i.e. position and rotation) expressed with respect to frame (a)...d_Pa_a = X_ba * d_Pb_b; - using the
>>operator;
The same concept can be used to chain coordinate transformations. For instance, if the transformation from frames c to b and from b to a are known, the overall frame rotation and displacement can be obtained as
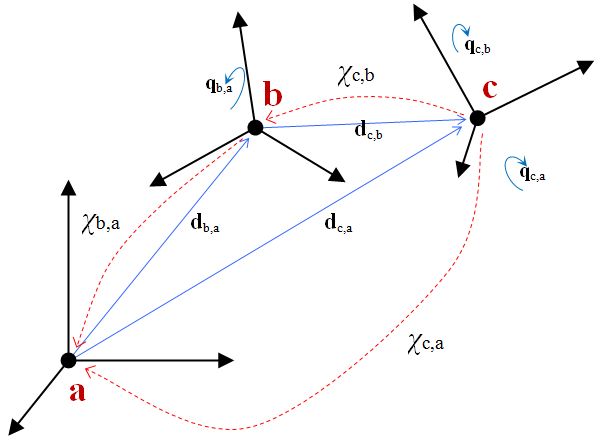
or, equivalently, by making use of the >> operator:
In Chrono, most of the transformation between ChCoordsys<>, ChFrame<> and ChFrameMoving<> (which is defined below) can be expressed in two equivalent ways:
- using the * operator RIGHT TO LEFT transformations, as in:
X_ca = X_ba * X_cb
- using the >> operator LEFT TO RIGHT transformations, as in:
X_ca = X_cb >> X_ba
The latter has some advantages:
- it is more 'intuitive' (see how the subscripts cb-ba follow a 'chain')
- it leverages the default compiler operation precedence rules (from left to right) to improve computational performance
For example if the first operand is a vector, as invnew = v >> X_dc >> X_cb >> X_ba, the default behavior of the compiler leads to a sequence of matrix-by-ChFrame operations returning temporary vectors. On the contrary, the * operator would create severalChFrame<>temporary objects, which would be slower.
One can also use the * or >> operators with other objects, for example using >> between a ChFrame Xa and a ChVector3 vb. The outcome of this operation is a new ChFrame object obtained by translating the old one by a vector vb:
The same holds for in-place operators *= or >>=, which can be used to translate or to rotate a ChFrame, or to transform entirely, depending on how it is used: with a ChVector3 or a ChQuaternion or another ChFrame. For example, to translate Xa by vector vb one writes:
Note that while the operators * and >> create temporary objects, that is not the case with *= or >>=, which leads to improved efficiency. In this context, a rule of thumb is to avoid:
- Operators * and >>
- Use of low-level functions such as TransformLocalToParent, TransformParentToLocal, etc.
Both the * and >> operations support an inverse transformation. Example: in the relation X_ca = X_cb >> X_ba; supposed that X_ca and X_cb are known and one is interested in computing X_ba. Pre-multiplying both sides of the equation by the inverse of X_cb yields
Note that the GetInverse operation might be less efficient than the less readable low-level methods, in this case TransformParentToLocal(), that is:
See chrono::ChFrame for API details.
ChFrameMoving
The chrono::ChFrameMoving object represents a coordinate system in 3D space, like a ChFrame, but it stores also information about the velocity and accelerations of the frame:
\[ \mathbf{c}=\{\mathbf{p},\mathbf{q},\dot{\mathbf{p}}, \dot{\mathbf{q}}, \ddot{\mathbf{p}}, \ddot{\mathbf{q}} \} \]
Note that using quaternion derivatives to express angular velocity and angular acceleration can be cumbersome. Therefore, this class also has the possibility of setting and getting such data in terms of angular velocity
\( \mathbf{\omega} \) and of angular acceleration \( \mathbf{\alpha} \) :
\[ \mathbf{c}=\{\mathbf{p},\mathbf{q},\dot{\mathbf{p}}, \mathbf{\omega}, \ddot{\mathbf{p}}, \mathbf{\alpha}\} \]
This can be shown intuitively with the following picture:
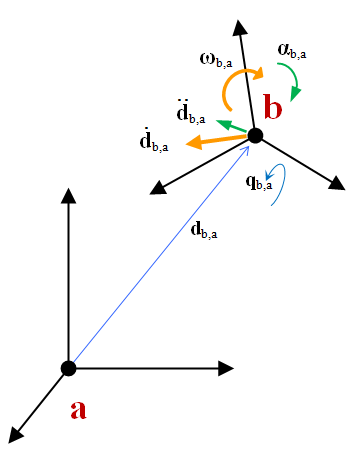
Note that 'angular' velocities and accelerations can be set/get both in the basis of the moving frame or in the absolute frame.
Example: A ChFrameMoving is created and assigned a non-zero angular velocity and linear velocity, also linear and angular accelerations are assigned.
A ChFrameMoving can be used to transform ChVector3 (points in space), a ChFrame, or ChFrameMoving objects. Velocities are also computed and transformed.
Example: The absolute velocity and angular velocity of c with respect to a can be computed if the transformation from b to a and from c to b is known:
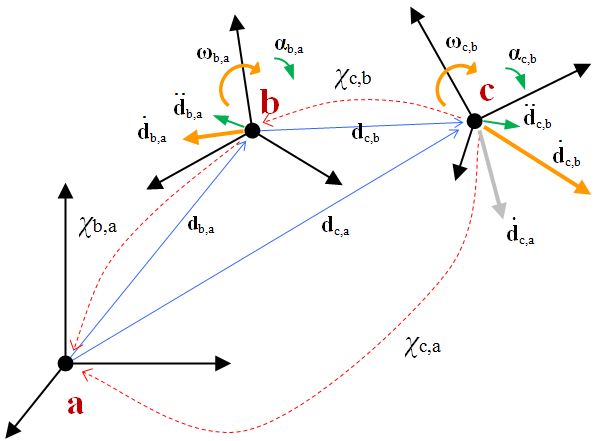
The case above translates in the following equivalent expressions, using the two alternative formalisms (Left-to-right based on >> operator, or right-to-left based on * operator):
This is exactly the same algebra used in ChFrame and ChCoordsys, except that this time also the velocities and accelerations are also transformed.
Note that the transformation automatically takes into account the contributions of complex terms such as centripetal accelerations, relative accelerations, Coriolis acceleration, etc.
The following is another example with a longer concatenation of transformations:
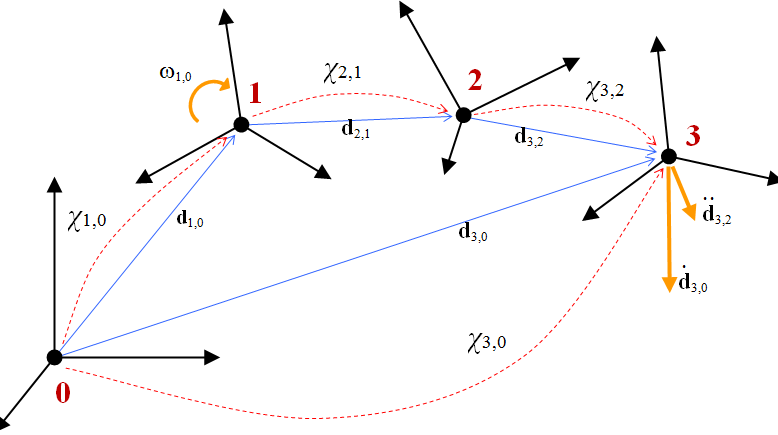
Note that one can also use the inverse of frame transformations, using GetInverse(), as seen for ChFrame.
Example: Computing the position, velocity and acceleration of the moving target 8 with respect to the gripper 6, expressed in the basis of the frame 6.
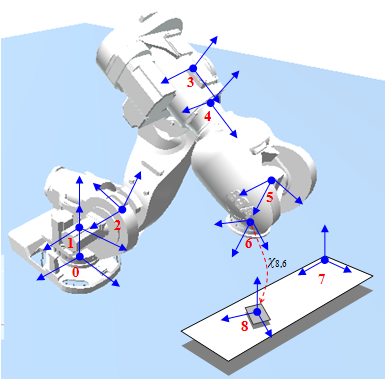
How would one compute X_86 knowing all others? Start from two equivalent expressions of X_80:
X_86>>X_65>>X_54>>X_43>>X_32>>X_21>>X_10 = X_87>>X_70;
also:
X_86>>(X_65>>X_54>>X_43>>X_32>>X_21>>X_10) = X_87>>X_70;
Post multiply both sides by inverse of (...), remember that in general
- X >> X.GetInverse() = I
- X.GetInverse() >> X = I,
where I is the identity transformation that can be removed, to finally get:
Example, based on the same figure: Computing velocity and acceleration of the gripper with respect to the moving target 8, expressed in the basis of reference frame 8.
See chrono::ChFrameMoving for API details.
ChMarker
ChMarker objects are auxiliary frames that have the specific feature of following the rigid body to which they are attached while potentially moving with respect to it.
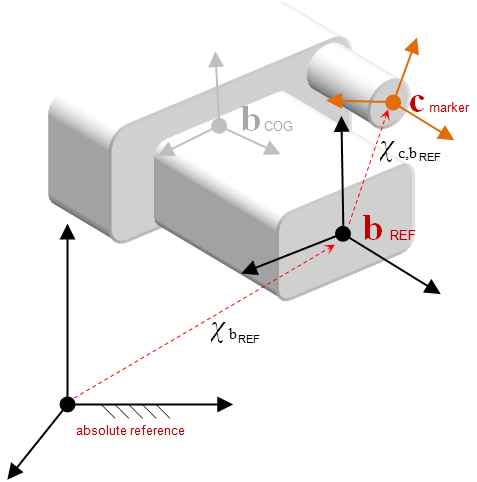
ChMarker are used most often in the ChLinkLock link family.
Theory
Additional details on the theoretical aspects of coordinate transformations in Chrono:
